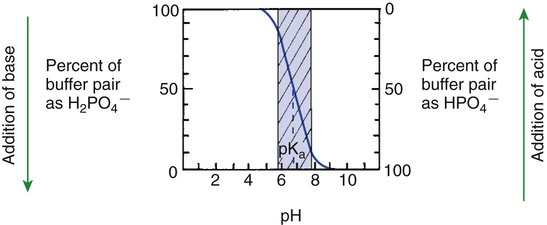
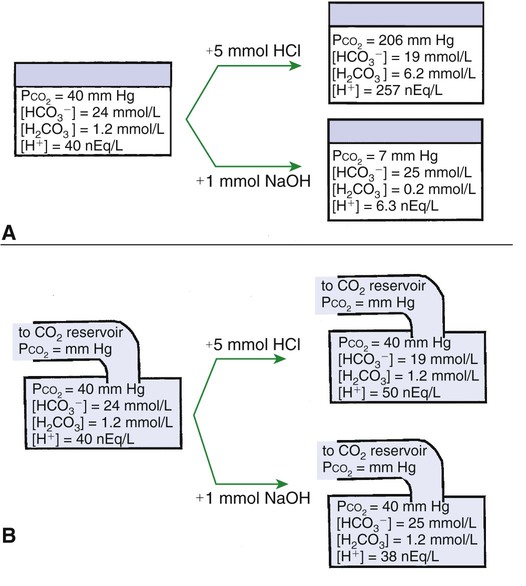
1. Relative constancy of the body’s pH is essential because metabolism requires enzymes that operate at an optimal pH. 2. Hydrogen ion concentration is measured as pH. 3. An acid can donate a hydrogen ion, and a base can accept a hydrogen ion. 4. Buffers are combinations of salts and weak acids that prevent major changes in pH. 5. Hemoglobin and bicarbonate are the most important blood buffers. 6. The first defense against a change in blood pH is provided by the blood buffers, but the lungs and kidneys must ultimately correct the hydrogen ion load. 7. Changes in ventilation can rapidly change carbon dioxide tension and therefore alter pH. 8. Metabolic production of fixed acids requires that the kidneys eliminate hydrogen ions and conserve bicarbonate. 9. Intracellular pH is regulated by buffers and ion pumps. 1. Acid-base abnormalities accompany many diseases, and the restoration of normal blood pH should be a consideration in the treatment of any disease. 2. Respiratory acidosis is caused by the accumulation of carbon dioxide, which decreases blood pH. 3. Respiratory alkalosis is caused by the loss of carbon dioxide, which increases blood pH. 4. Metabolic acidosis is caused by the accumulation of fixed acids or the loss of buffer base, which decreases blood pH. 5. Metabolic alkalosis is caused by the excessive elimination of hydrogen ions or by the intake of base, such as bicarbonate, which increases blood pH. 6. Respiratory compensations for acid-base abnormalities occur rapidly; renal compensations occur over several hours. 7. Hydrogen and potassium ions are interrelated in acid-base homeostasis. 8. The diagnosis of acid-base disturbances depends on interpretation of measurements of arterial blood pH and carbon dioxide tension, from which bicarbonate concentration and total buffer base are calculated. 9. Over the years, many terms have been used to explain acid-base balance. Taking logarithms of both sides of this equation results in: Rearrangement of this equation yields: However, −log[H+] is pH and −logKa is called pKa; therefore: Figure 52-1 shows the change in pH that results when acid is added to a phosphate buffer with a pKa of 6.8. This is a graphic presentation of the Henderson-Hasselbalch equation. Initially, as acid is added, there is a large decrease in pH. As considerably more acid is added to the solution, the pH changes little. H+ ions combine with HPO42− and form H2PO4−. Finally, the pH decreases considerably. The zone over which the pH changes little as acid is added (i.e., where buffering capacity is optimal) is within ±1 pH unit of the pKa. Note that when the pH equals the pKa, 50% of the buffer has been consumed. From this buffer curve, it is obvious that an effective buffer must have a pKa within ±1 pH unit of the solution in which it operates. Thus the optimal blood buffers should have a pKa between 6.4 and 8.4. In addition, buffers must be sufficiently plentiful to be effective. The other blood buffer with an optimal pKa is the HPO42−/H2PO4− system, with a pKa of 6.8 (see Figure 52-1). The normally low phosphate concentration in the blood makes this buffering system quantitatively unimportant; however, it is important in the renal tubules, where phosphate becomes concentrated. Plasma proteins also provide a small amount of blood buffering. Figure 52-2 shows the value of this open system in maintaining body pH. It should be noted that the concentration of H2CO3 ([H2CO3]) in solution is directly proportional to the carbon dioxide tension (PCO2); 1 molecule of H2CO3 is in equilibrium with 340 molecules of CO2. Therefore, [H2CO3] can be calculated as 0.03 × PCO2. In Figure 52-2, A and B, top panels, 5 mmol of hydrochloric acid is added to plasma. Figure 52-2, A, shows what happens if the PCO2 and thus [H2CO3] is held constant. In such a closed system, the 5 mmol of HCl reacts with 5 mmol of HCO3− to form 5 mmol of H2CO3. As a consequence of this reaction, [HCO3−] decreases from 24 to 19 mmol/L, [H2CO3] increases from 1.2 to 6.2 mmol/L, and PCO2 increases from 40 to 206 mm Hg. Using the law of mass action, one can calculate that [H+] increases from 40 to 257 nEq/L or, stated in other terms, pH decreases from 7.4 to 6.5. If the system is open, however (as it is in the top panel of Figure 52-2, B) carbon dioxide evolves to the environment as fast as it is produced so that PCO2 and therefore [H2CO3] remain constant, then [H+] increases to only 50 nEq/L and the pH decreases only to 7.3. The lower panel in Figure 52-2, B, shows similar advantages to the open system when a strong base is added to the buffer system. Under most conditions, the body functions as an open system with regard to the HCO3−/H2CO3 system so that pH changes are minimized. When tissues are ischemic, however, they have no connection to the lungs, so CO2 cannot be eliminated. The ischemic tissue then functions as a closed system, and pH changes within the tissue can therefore be drastic.
Acid-Base Homeostasis
Buffers Are Combinations of Salts and Weak Acids That Prevent Major Changes in pH
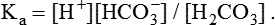
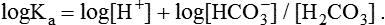
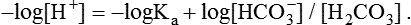
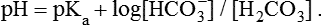
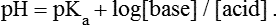
Hemoglobin and Bicarbonate Are the Most Important Blood Buffers
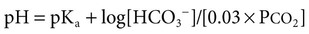
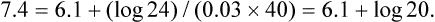
The First Defense Against a Change in Blood pH Is Provided by the Blood Buffers, but the Lungs and Kidneys Must Ultimately Correct the Hydrogen Ion Load
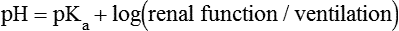
![]()
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree