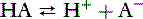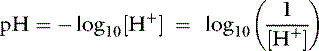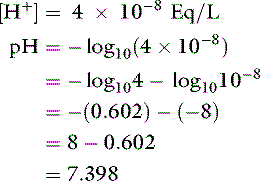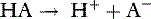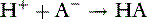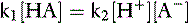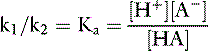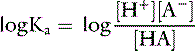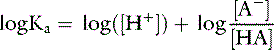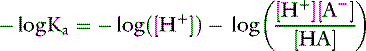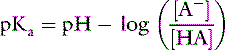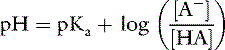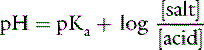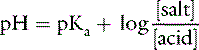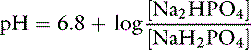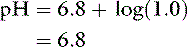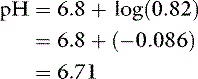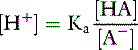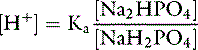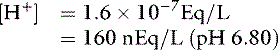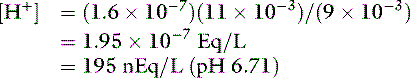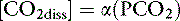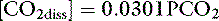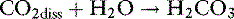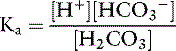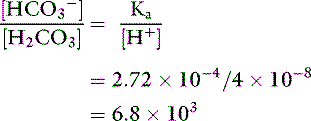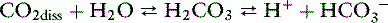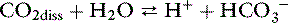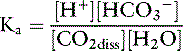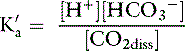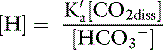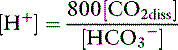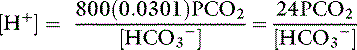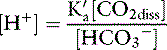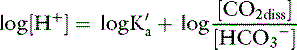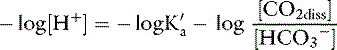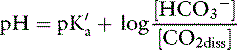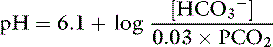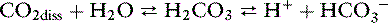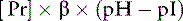Concept of acidity

The most commonly used concept of acids and bases is that of Brönsted and Lowry, who stated that an acid is a proton donor and a base a proton acceptor. In the following equation, HA is an acid and A⁻ is a base:

In aqueous solutions, protons or H⁺ ions are normally bound by electrostatic interaction to H₂O, resulting in the formation of hydronium ions, designated H₃O⁺. Conventionally, however, the term hydrogen ion and the symbol H⁺ are used to refer to protons in aqueous solutions.

The acidity of a solution refers to the chemical activity of its constituent H⁺ ions. Chemical activity is related to chemical concentration by the activity coefficient, a factor that varies directly with temperature and inversely with the ionic strength of the solution. Physiologic control of body temperature and osmolality, and the dilute nature of body fluids, result in this factor being near unity, and the difference between activity and concentration is negligible in body fluids.

The concentrations of the most important electrolytes in body fluids (e.g., Na⁺, K⁺, Cl⁻, HCO₃⁻) are in the range of milliequivalents per liter, whereas the concentration of H⁺ is in the range of nanoequivalents per liter. That is, hydrogen ions are present at one-millionth the concentration of other electrolytes. What, then, accounts for the emphasis on hydrogen ions in biology and medicine? The answer lies in the fact that hydrogen ions are highly reactive. The proteins of the body have many dissociable groups. These may gain or lose protons as [H⁺] changes, resulting in alterations in charge and molecular configuration that may adversely affect protein structure and function. The [H⁺] of body fluids must be kept constant so that detrimental changes in enzyme function and cellular structure do not occur. The range of [H⁺] compatible with life is 16 to 160 nEq/L.

Concept of pH

The concept of pH was introduced by Sørensen to allow easier notation for the wide range of [H⁺] found in chemical systems. The term pH is defined as the negative base 10 logarithm of the hydrogen ion concentration expressed in equivalents per liter or the base 10 logarithm of the reciprocal of the hydrogen ion concentration:

Thus, at the normal extracellular fluid (ECF) [H⁺] of 40 nEq/L (4 × 10⁻⁸ Eq/L):

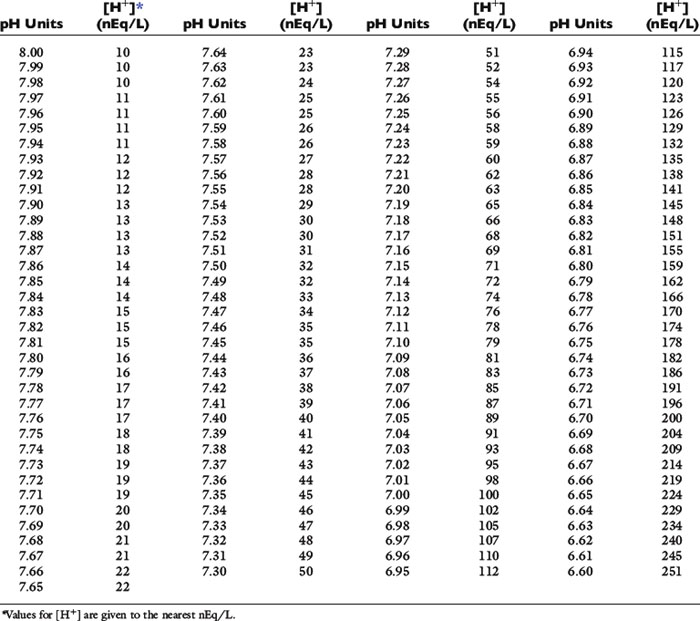
There is an inverse relationship between pH and [H⁺]: the greater the [H⁺], the lower the pH. Furthermore, pH and [H⁺] vary not linearly with one another but exponentially as shown in Figure 9-1. The [H⁺] for a given pH within the physiologic range is given in Table 9-1.

Figure 9-1 Exponential relationship between [H⁺] and pH.

(From Madias NE, Cohen JJ. Acid-base chemistry and buffering. In: Cohen JJ, Kassirer JP, editors. Acid-base. Boston: Little, Brown, 1982: 5.)

Table 9-1 Conversions Between pH and [H⁺]

Law of mass action

The law of mass action states that the velocity of a reaction is proportional to the product of the concentrations of the reactants. For the acid just described, there are two opposing reactions:

The velocity of the first reaction can be written:

At equilibrium, the rates of the two opposing reactions exactly counterbalance one another and the two velocities are equal:

Rearranging and substituting a new constant, K_a, the ionization, or dissociation, constant for the acid HA:

The ionization, or dissociation, constant for an acid is an indication of the strength of that acid. A large value for K_a means that [H⁺] and [A⁻] are much greater than [HA]; that is, the acid is a strong one and is largely dissociated. A small value for K_a means that [H⁺]and [A⁻] are much smaller than [HA]; that is, the acid is a weak one and little of it is dissociated. Hydrochloric acid (HCl) and sulfuric acid (H₂SO₄) are strong acids and dissociate almost completely in aqueous solutions, whereas NH₄⁺ is a weak acid (i.e., it is a strong base) and dissociates to a small extent.

Taking the base 10 logarithm of both sides of the dissociation equilibrium equation yields:

Multiplying by −1 yields:

Applying the concept of pH to both the hydrogen ion concentration and dissociation constant, K_a:

This is the commonly used Henderson-Hasselbalch form of the dissociation equilibrium equation. Occasionally, the term salt or base is substituted for A⁻ and the term acid for HA:

Concept of buffering

A buffer is a compound that can accept or donate protons (hydrogen ions) and minimize a change in pH. A buffer solution consists of a weak acid and its conjugate salt. When a strong acid is added to a buffer solution containing a weaker acid and its salt, the dissociated protons from the strong acid are donated to the salt of the weak acid and the change in pH is minimized.

Consider an aqueous solution with equal amounts of Na₂HPO₄ and NaH₂PO₄. The pK_a for this buffer pair is 6.8:

If the amounts of Na₂HPO₄ and NaH₂PO₄ are equal, their ratio is 1.0:

Consider adding 1 mmol of HCl to this solution. The protons from the HCl are donated to the salt of the buffer pair (Na₂HPO₄), converting it to its conjugate acid (NaH₂PO₄). If 10 mmol of each phosphate salt was present initially, the new ratio of Na₂HPO₄/NaH₂PO₄ would be 9/11 or 0.82 and:

By contrast, an aqueous solution containing 1 mmol/L HCl (10⁻³Eq/L) would have a pH of 3.0.

By solving the dissociation equilibrium equation for [H⁺], the same can be shown:

For the previously described solution of sodium phosphate:

The K_a for this reaction is 1.6 × 10⁻⁷ Eq/L, and if there are equal amounts of the two phosphate salts present ([NaH₂PO₄] = [Na₂HPO₄]):

After addition of 1 mmol of HCl:

By contrast, an aqueous solution containing 1 mmol/L HCl would have [H⁺] = 0.001 mol/L or 1 million nmol/L. Thus, 99.98% of the added hydrogen ions have been buffered by the sodium phosphate solution.

If the amount of strong acid (e.g., HCl) or base (e.g., NaOH) added to a solution of a weak acid and its salt (i.e., a buffer solution) is plotted against pH, the resulting relationship is called a titration or buffer curve (Fig. 9-2). The curve is sigmoidal, and its slope is greatest in the midregion, over which the curve is approximately linear. In the pH range associated with the midregion of the curve, the change in pH is smallest for a given amount of added acid or base and buffer capacity is greatest at the midpoint of the curve. At this point, there are equal amounts of the weak acid and its conjugate salt, and as shown by the Henderson-Hasselbalch equation, pH = pK_a. The region of best buffer capacity extends approximately 1.0 pH unit on either side of the pK_a. Thus, a buffer is most effective within one pH unit of its pK_a. The pK_a values for some important biologic compounds are listed in Table 9-2.

Figure 9-2 Titration curve for an aqueous solution containing a phosphate buffer.

(From Ruch TC, Patton HE (eds): Physiology and biophysics, 20^th edition, Saunders, Philadelphia, 1974.)

Table 9-2 pK_a Values of Biologically Important Compounds*

* Compounds with pK_a values in the range of 6.4-8.4 are most useful as buffers in biologic systems. The pK_a values for the imidazole group of histidine and for α-amino (amino-terminal) amino groups are for those side groups in proteins. The pK_a range for organ phosphates refers to such intracellular compounds as adenosine triphosphate, adenosine diphosphate, and 2,3-diphosphoglycerate.

Isohydric principle

Regardless of the number of buffers present, a solution can have only one [H⁺] and one pH. Using the law of mass action or the Henderson-Hasselbalch equation, the ratio of acid to salt forms of any buffer in the solution can be calculated. This has been called the isohydric principle. The implication of the isohydric principle is that the behavior of any buffer pair in a complex solution can be predicted by knowledge of the dissociation constant and concentrations of any one buffer pair. In clinical practice, the bicarbonate–carbonic acid buffer pair is the one used to monitor acid-base balance in body fluids.

The relative importance of a given buffer in the body is based on its concentration in the relevant body fluid, its pK_a, and the prevailing [H⁺] (40 nmol/L in ECF). The bicarbonate–carbonic acid system is unique among buffers in that carbonic acid is in equilibrium with dissolved CO₂, the concentration of which normally is kept constant by alveolar ventilation.

The bicarbonate–carbonic acid system: physical chemistry

Gaseous CO₂ produced in the tissues is soluble in water, and the concentration of dissolved CO₂ in body fluids is proportional to the partial pressure of CO₂ in the gas phase (Pco₂):

Dissolved CO₂ combines with water to form carbonic acid:

The uncatalyzed reaction proceeds slowly, but its rate is dramatically increased by the enzyme carbonic anhydrase, which is present in abundance in the body (e.g., red cells, renal tubular cells). In the body, therefore, the hydration of CO₂ to form H₂CO₃ reaches equilibrium almost instantaneously. Normally, the equilibrium is so far to the left that there are approximately 340 molecules of dissolved CO₂ for each molecule of carbonic acid.⁴²

The dissociation of carbonic acid can be expressed using the law of mass action:

K_a for this reaction is 2.72 × 10⁻⁴ mol/L (pK_a=3.57). The ratio of bicarbonate to carbonic acid at the normal [H⁺] of body fluids can be calculated by rearranging this equation:

Thus, at [H⁺] = 40 nmol/L (pH 7.40), there are 6800 bicarbonate ions and 340 molecules of dissolved CO₂ for each molecule of carbonic acid.

The reaction of dissolved CO₂ in aqueous body fluids can be summarized as:

However, the number of carbonic acid molecules is negligible compared with the number of dissolved CO₂ molecules and HCO₃⁻ ions. Therefore, this equation can be simplified as:

The law of mass action for this equilibrium can be expressed as:

The concentration of water in dilute body fluids remains virtually unchanged by this reaction and can be incorporated into K_a to yield another constant, K′_a:

Solving for [H⁺] yields:

In body fluids at 37˚ C, K′_a is approximately equal to 8 × 10⁻⁷ mol/L and p K′_a equals 6.1. An approximate value of 6.1 for this p K′_a is valid at temperatures ranging from 30° to 40° C (86 to 104° F) and pH values ranging from 7.0 to 7.6.³⁷

A formula for [H⁺] in nanomoles per liter or nanoequivalents per liter is obtained by expressing K′_a in nanomoles per liter or nanoequivalents per liter:

Using the solubility coefficient for carbon dioxide yields:

This is the Henderson equation and has been used extensively in the clinical evaluation of acid-base disturbances. It shows clearly that the [H⁺] (and thus pH) of body fluids is determined by the ratio of Pco₂ to HCO₃⁻ concentration. The Henderson-Hasselbalch equation is derived by expressing [H⁺] and K′_a in moles per liter or equivalents per liter and converting the equation to logarithmic form:

Multiplying by −1, we obtain:

Substituting 6.1 for the value of pK′a and applying the solubility coefficient for CO₂, we obtain:

This is the clinically relevant form of the equation and shows that in body fluids, pH is a function of the ratio between HCO₃⁻ concentration and Pco₂.

Body buffers

Body buffers can be divided into bicarbonate, which is the primary buffer system of ECF, and nonbicarbonate buffers (e.g., proteins and inorganic and organic phosphates), which constitute the primary intracellular buffer system. Bone is a prominent source of buffer and can contribute calcium carbonate and, to a lesser extent, calcium phosphate during chronic metabolic acidosis. Bone may even account for up to 40% of the buffering of an acute acid load in the dog.⁹ After administration of NaHCO₃, carbonate can be deposited in bone.

Proteins as buffers

Plasma proteins play a limited role in extracellular buffering, whereas intracellular proteins play an important role in the total buffer response of the body. The buffer effect of proteins is the result of their dissociable side groups. For most proteins, including hemoglobin, the most important of these dissociable groups is the imidazole ring of histidine residues (pK_a, 6.4 to 7.0). Amino-terminal amino groups (pK_a, 7.4 to 7.9) also contribute somewhat to the buffer effect of proteins. Other side groups are relatively unimportant because their pK_a values are either too high or too low to be useful in the normal physiologic range of pH. The pK_a values for the dissociable groups of proteins are listed in Table 9-3.

Table 9-3 pK′a Values for Dissociable Groups Found in Proteins

Dissociable Group (Amino Acid)	pK′a
α-Carboxyl	3.6-3.8
β-Carboxyl (aspartic acid)	≈4.0
γ-Carboxyl (glutamic acid)	≈4.0
Imidazole (histidine)	6.4-7.0
α-Amino	7.4-7.9
Sulfhydryl (cysteine)	≈9.0
ε-Amino (lysine)	9.8-10.6
Phenolic (tyrosine)	8.5-10.9
Guanidino (arginine)	11.9-13.3

From Madias NE, Cohen JJ: Acid-base chemistry and buffering. In Cohen JJ, Kassirer JF, editors: Acid-base, Boston, 1982, Little, Brown & Co., p. 16.

Hemoglobin is responsible for more than 80% of the nonbicarbonate buffering capacity of whole blood, whereas plasma proteins contribute 20%. Of the plasma proteins, albumin is much more important than are the globulins. The buffer value of albumin is 0.12 to 0.14 mmol/g/pH unit, whereas that of globulins is 0 to 0.08 mmol/g/pH unit.^38,69,71 The difference results from a larger number of histidine (Fig. 9-3) residues in albumin.

Figure 9-3 The imidazole group of histidine.

(From Madias NE, Cohen JJ. Acid-base chemistry and buffering. In: Cohen JJ, Kassirer JP, editors. Acid-base. Boston: Little, Brown, 1982: 16.)

The isoelectric point (pI) is the pH at which a substance has no tendency to move in an electric field and thus has no net charge. For proteins, this means that the sum of the charges on the negative side groups (e.g., R–COO−) equals the sum of the charges on the positive side groups (e.g., R–NH₃⁺). At physiologic pH (7.4), plasma proteins are polyanions because their pIs range from 5.1 to 5.7. The net negative charge on plasma proteins in mEq/L can be calculated as:³⁸

where [Pr] is the concentration of plasma proteins in grams per liter, β is the buffer value of plasma proteins in millimoles per gram per pH unit, pH is the ECF pH, and pI is the isoelectric point of plasma proteins. Using this formula, it can be calculated that, at a normal plasma protein concentration of 7 g/dL, average buffer value of 0.1 mmol/g/pH unit, and pI range of 5.1 to 5.7, plasma proteins contribute 12 to 16 mEq/L of negative charge. In dogs, the mean contribution of charge by plasma proteins is approximately 16 mEq/L.^16,76

Physiologic lines of defense in acid-base disturbances

An overview of the body buffer response is provided by contrasting the body’s response to a nonvolatile, or fixed, acid (e.g., HCl) and its response to the volatile acid CO₂. The hydrogen ions from a fixed acid load immediately titrate bicarbonate ions in ECF and then titrate intracellular buffers (e.g., proteins, phosphates). This physicochemical response occurs within minutes and protects ECF pH. Alveolar ventilation is stimulated, and Pco₂ is decreased to below normal. This response, which begins immediately and is complete within hours, minimizes the change in pH because the ratio of HCO₃⁻ to Pco₂ is normalized. Finally, the kidneys regenerate titrated HCO₃⁻, pH increases, alveolar ventilation decreases, and Pco₂ returns to normal. The renal response begins within hours but requires 2 to 5 days to reach maximal effectiveness.

The volatile acid CO₂ cannot be buffered by HCO₃⁻, and the hydrogen ions resulting from the dissociation of carbonic acid must titrate intracellular buffers, such as proteins (especially hemoglobin in red cells) and phosphates. Renal adaptation is characterized by increased HCO₃⁻ reabsorption and net acid excretion, mechanisms that require 2 to 5 days to achieve maximal effectiveness. The buffer response of the body to the primary acid-base disorders is considered in more depth in the chapters on those disorders (see Chapters 10 and 11).

Terminology

The terms acidosis and alkalosis refer to the pathophysiologic processes that cause net accumulation of acid or alkali in the body. The terms acidemia and alkalemia refer specifically to the pH of ECF. In acidemia the ECF pH is lower than normal, and the [H⁺] is higher than normal. In alkalemia the ECF pH is higher than normal, and the [H⁺] is lower than normal. The distinction between these terms is important. For example, a patient with chronic respiratory alkalosis may have a blood pH within the normal range because of effective renal compensation in this setting. Such a patient has alkalosis but does not have alkalemia. Patients with mixed acid-base disturbances can have blood pH values within the normal ranges as a result of the presence of two counterbalancing acid-base disturbances (see the following section on Simple and Mixed Acid-Base Disorders).

Primary acid-base disturbances

Acidosis and alkalosis can each be of metabolic or respiratory origin, and as a result, there are four primary acid-base disturbances: metabolic acidosis, respiratory acidosis, metabolic alkalosis, and respiratory alkalosis. The metabolic disturbances refer to a net excess or deficit of nonvolatile, or fixed, acid, whereas the respiratory disturbances refer to the net excess or deficit of volatile acid (dissolved CO₂).

Metabolic acidosis is characterized by a decreased plasma HCO₃⁻ concentration and decreased pH (increased [H⁺]) caused by either HCO₃⁻ loss or buffering of a noncarbonic (nonvolatile or fixed) acid. Metabolic alkalosis is characterized by an increased plasma HCO₃⁻ concentration and increased pH (decreased [H⁺]), usually caused by a disproportionate loss of chloride ions from the body (i.e., loss of fluid with a chloride concentration greater than that of ECF) or hypoalbuminemia (because albumin is a weak acid). In the absence of volume depletion or renal dysfunction, it is extremely difficult to produce metabolic alkalosis by administration of alkali. Respiratory acidosis is characterized by increased Pco₂ (hypercapnia) caused by alveolar hypoventilation. Respiratory alkalosis is characterized by decreased Pco₂ caused by alveolar hyperventilation (hypocapnia). In one study, metabolic acidosis was the most common acid-base disturbance encountered in dogs.¹⁷

Each primary metabolic or respiratory acid-base disturbance is accompanied by a secondary, or adaptive, change in the opposing component of the system (Table 9-4). The adaptive response involves the component opposite the one disturbed and returns the pH of the system toward but not completely to normal. Overcompensation does not occur. For example, metabolic acidosis is accompanied by a secondary or adaptive respiratory alkalosis. Respiratory acidosis is accompanied by a secondary or adaptive metabolic alkalosis.

Table 9-4 Characteristics of Primary Acid-Base Disturbances

Simple and mixed acid-base disorders

An acid-base disorder is said to be simple if it is limited to the primary disorder and the expected secondary, or adaptive, response. The magnitude of the expected responses is considered in detail in the chapters devoted to the primary acid-base disorders (see Chapters 10 and 11). A mixed acid-base disorder is one that is characterized by the presence of at least two separate primary acid-base abnormalities occurring in the same patient. A mixed acid-base disorder should be suspected whenever the secondary, or adaptive, response exceeds or falls short of that expected. In dogs, for example, the expected response to metabolic acidosis is a 0.7-mm Hg decrease in Pco₂ for each 1.0-mEq/L decrement in plasma HCO₃⁻ concentration caused by metabolic acidosis (see Chapter 10 for more details).

Consider a dog with these normal blood gas values: p. 7.39, [H⁺] = 41 nEq/L, [HCO₃⁻] = 21 mEq/L, and Pco₂ = 36 mm Hg. This dog becomes ill and is observed to have the following blood gas values: p. 7.22, [H⁺] = 60 nEq/L, [HCO₃⁻] = 14 mEq/L, and Pco₂ = 35 mm Hg. If the dog had a simple metabolic acidosis, using the rule of thumb described before, we would have expected the following results: p. 7.27, [H⁺] = 53 nEq/L, [HCO₃⁻] = 14 mEq/L, and Pco₂ = 31 mm Hg. Thus, the dog has a mixed acid-base disorder characterized by both metabolic and respiratory acidoses.

Consider a patient with the following blood gas values: p. 7.40, [H⁺] = 40 nEq/L, [HCO₃⁻] = 31 mEq/L, and Pco₂ = 51 mm Hg. This patient is neither alkalemicnoracidemic because blood pH is 7.40; however, based on the Pco₂ and [HCO₃⁻], the patient is not normal. This patient has a mixed disorder characterized by metabolic alkalosis and respiratory acidosis. The two disorders have counterbalancing effects, resulting in a normal pH. Mixed acid-base disorders are considered in detail in Chapter 12.