and Christopher D. Kroenke1, 2
(1)
Department of Behavioral Neuroscience, Advanced Imaging Research Center, Oregon Health and Science University, Portland, OR, USA
(2)
Oregon Health and Science University, Portland, OR 97239, USA
Abstract
Diffusion tensor imaging (DTI) is a magnetic resonance imaging (MRI) technique that provides information about cellular microstructure through measurements of water diffusion. Because inferences about neuroanatomy can be made from DTI, this methodology has been used to characterize cellular morphological changes associated with development of the cerebral cortex. Currently, however, the specific anatomical changes associated with DTI measurements directed at the cerebral cortex are incompletely characterized. Here, data collected in several laboratories, investigating five species (mouse, rat, ferret, baboon, and human), are compared to determine whether similarities in the trajectory of DTI measurements with development exist in the literature. Specifically, rates of change in fractional anisotropy (FA) of water diffusion were compared to rates of neuroanatomical development (based on the occurrence of specific neural events) in each species. In all species, decreases in FA with development were accurately approximated by fitting data to the same mathematical expression of exponential decay. Additionally, a high degree of correlation was found between rates of FA decay and rates of neuroanatomical development. This suggests that a common mechanism underlies decreases in FA with development across species. These results have two major implications. The ability of DTI to detect changes in neuroanatomy in the normal developing cerebral cortex introduces the potential for the use of this methodology in detecting cortical abnormalities associated with various developmental disorders. Additionally, the comparable patterns of neurodevelopment, and hence FA, across species imply that DTI methodology applied in non-human species can provide information about the human condition.
Key words
Cerebral cortex, developmentcomparative, diffusion tensor imaging, prenatal1 Introduction
Magnetic resonance imaging (MRI) is a non-invasive imaging technique that holds much potential for investigating brain disorders and brain development. A subclass of MRI experiments collectively termed diffusion tensor imaging (DTI) is particularly well suited to study the cellular-level bases of tissue changes associated with development and pathology. In DTI experiments, the image intensity recorded by MRI is rendered sensitive to diffusion-mediated displacement of water molecules over distances of approximately 10 μm in the tissue under study (1, 2). These measurements are extremely powerful because biological membranes impede water displacement due to diffusion (3), and thus the cellular-scale structure of tissue is reflected in water diffusion measurements. In tissue that is highly ordered on the cellular scale, water diffusion exhibits a directional dependence (4). Directional dependence in molecular diffusion is termed diffusion anisotropy and is most frequently measured within the context of MRI through application of the diffusion tensor formalism (5–7). The extent of diffusion anisotropy reflects the degree of cellular-scale order in tissue and is frequently quantified in terms of fractional anisotropy (FA), a parameter that ranges from 0 (isotropic diffusion, unstructured tissue) to 1 (extremely anisotropic diffusion, well-ordered tissue).
Several recent studies of brain development have provided evidence that DTI strategies are of potential utility for characterizing the development of the cerebral cortex. Water diffusion anisotropy decreases with maturation of the cerebral cortex, and it is believed that the observed changes in diffusion anisotropy reflect cellular morphological changes relevant to cortical development. In the immature state, at a time when cortical FA is high, neurons are undifferentiated and highly radially oriented (8, 9); subsequently, neurons undergo morphological differentiation, and it has been found that this event in cortical development is temporally associated with a decrease in diffusion anisotropy (10, 11).
Significant diffusion anisotropy in the immature cerebral cortex was first observed in studies of cats (12) and pigs (13). More recently, such measurements have been extended to several other species including humans. However, a systematic comparison of the rate of FA changes has yet to be referenced to species-specific rates of brain development, estimated in comparative analyses of timing of developmental events (14–16). A comparison of DTI studies to independent studies of neuroanatomical development could therefore provide support that a common underlying developmental process gives rise to patterns observed in DTI measurements. DTI-based studies of cortical development are reviewed in the following sections, and methodological issues associated with differences in acquisition and analysis procedures among laboratories are discussed. To obtain independent experimental confirmation that changes in cortical diffusion anisotropy occur at a rate that is consistent with the rate of morphological differentiation of the cerebral cortex across species, the comparative DTI data reviewed here are referenced to species-specific rates of brain development estimated from comparative analyses of developmental event timings reported in classical anatomical studies (14–16).
2 The Phenomenon of Anisotropic Water Diffusion Within the Developing Cerebral Cortex
2.1 Water Diffusion Is Anisotropic Within Immature Cortical Gray Matter
Immediately following migration of pyramidal neurons from ventricular zones of the forebrain to the cortical plate, neurons exhibit simple morphology characterized by elongated cell somas and undifferentiated, radially oriented apical dendrites (9, 17). As the cerebral cortex matures, obliquely oriented collaterals of apical dendrites, basilar dendrites, and axons arborize to provide a scaffold for the formation of functional synapses (18). Changes in water diffusion anisotropy take place along with these cellular-level morphological transformations. In the immature cortex, preferential restriction of diffusion in directions parallel to the pial surface and relative lack of restriction in directions parallel to apical dendrites of pyramidal neurons (10–13, 19) are thought to be the primary causes of the prominent diffusion anisotropy seen at this time. As morphological differentiation occurs within the developing cerebral cortex, cortical FA decreases. Diffusion within mature cortex is nearly uniformly restricted in all directions, and diffusion anisotropy is measurable but subtle (20, 21). The temporally coincident evolution of cortical diffusion anisotropy with morphological development is schematized in Fig. 13.1 (10).
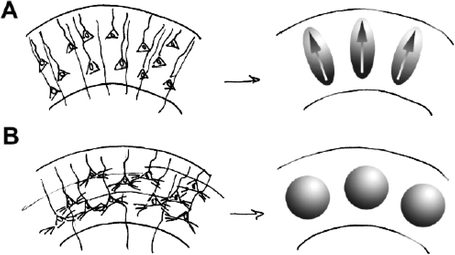

Fig. 13.1.
Hypothesized relationship between cortical neuronal differentiation and cortical diffusion anisotropy, taken from (10) by permission of Oxford University Press. (a) The left image displays neurons in the immature cortex that are undifferentiated and radially organized. It is hypothesized that this neuroanatomical organization causes water diffusion in the immature cortex to be highly directionally dependent, as represented by the ellipsoidal shapes on the right. (b) The left image is an example of neuronal organization in the mature cortex, wherein neurons are highly differentiated and much of the radial organization found at earlier stages of development is lost. It is hypothesized that the high degree of differentiation of neural components in the mature cortex leads to highly isotropic water diffusion represented by the spherical shapes on the right.
2.2 Temporal, Laminar, and Regional Patterns in the Loss of Cortical Diffusion Anisotropy with Development Coincide with Morphological Differentiation of Neurons
Although there is a strong association between the loss of cortical diffusion anisotropy and morphological differentiation of the cerebral cortex, the ability to interpret FA values within the developing cerebral cortex in terms of the underlying anatomical properties of brain tissue will require a quantitative link between FA changes and specific cellular morphological changes to be established. The component of cerebral cortex termed the neuropil, which consists of axons, dendrites, and associated extracellular space, represents 70–80% of the cerebral cortical volume fraction at maturity (22, 23). Given the relative sizes (volume fractions) of other elements such as glial cells (3.6% (23)), vasculature (4.3% (23)), and neuron cell somas (22% (23)), it has been proposed that the loss of cortical diffusion anisotropy with brain maturation can be attributed to morphological differentiation of the neuropil (Fig. 13.1) (10).
If cortical FA reflects the degree of differentiation of the neuropil rather than some other anatomical transformation, then FA would be expected to depend directly on the age of neurons within a given cortical region. Laminar (8) and regional (24, 25) patterns of neurogenesis have been extensively characterized in several species and are known to produce gradients in neuron age throughout the cerebral cortex. Previously, laminar and regional patterns of cortical FA have been examined at multiple stages of development following neurogenesis in an attempt to evaluate whether morphological properties of the neuropil determine cortical FA values in immature cortex.
Pyramidal neurons of the cerebral cortex are generated in an inside–out manner; neurons of deep cortical layers are born on earlier dates than neurons of more superficial layers (8). As a result, there is a laminar gradient in the age of these cells. Correspondingly, at early stages of cortical development, neurons of deep cortical cell layers have developed more extensive networks of obliquely oriented collateral branches of apical and basal dendrites than have neurons of superficial cell layers (17, 18). Based on these observations, a laminar gradient in cortical diffusion anisotropy would be expected, with superficial layers exhibiting higher anisotropy than deeper layers. Examination of the laminar dependence of cortical FA in fetal baboon brain provides evidence that a superficial-to-deep, high-to-low intracortical FA gradient exists (26, 27). Laminar gradients in FA have also been documented in rat cerebral cortex (28, 29).
A regional gradient in neurogenesis has also been described, in which neurons of a given cortical lamina are born earlier near the source of a transverse neurogenetic gradient (TNG (24, 25)) than at distal extremes of the cerebral cortical sheet. The neurodevelopmental mechanism giving rise to the TNG of cortical pyramidal neurons has not yet been elucidated, however the TNG source within the cortical sheet has been mapped onto models of the cortical surface for rodent species (24, 30), carnivores (ferrets (31, 32) and cats (33)), and primates (9). In ferrets and cats, the TNG gives rise to a 5-day age difference between neurons of a given lamina located at the TNG source and neurons located at the occipital pole (31–33). In the ferret (34), cortical FA values measured at ages P6 through adulthood were fitted to a model in which FA decreases exponentially with postnatal age following migration of pyramidal neurons to the cortical plate. From this analysis, it was found that the difference in FA between the TNG source and occipital pole corresponds to an age difference of 5 days, in agreement with previous histological estimates (31–33) and in close correspondence to differences in the ages of layer II neurons estimated by autoradiographic cell-birthdating studies of ferret somatosensory and visual cortical areas (35, 36). Similar rostral/lateral to caudal/dorsal cortical FA patterns corresponding to the TNG have also been observed in rat (28), baboon (27), and human (37).
Quantitative characterizations of laminar and regional patterns of cortical FA have thus established a correspondence with the age of pyramidal neurons within ferrets and baboons. This association is suggestive that a relationship exists between changes in cortical FA and morphological development of the neuropil. To provide further evidence of this potential relationship, a comparative analysis of data published from several laboratories is presented here to determine whether FA changes observed across species correspond to a common stage of brain development.
2.3 Application of Diffusion Anisotropy to Monitor Cerebral Cortical Development Is a Potential Strategy to Use DTI for Early Detection of Neurodevelopmental Disorders
A morphological abnormality common to individuals affected by a diverse array of neurodevelopmental disorders has been observed in which dendritic arbors of the early developing cerebral cortex are less elaborate than in age-matched control individuals (reviewed by Kaufmann and Moser (38) and in a special issue of Cerebral Cortex (39)). Simplified cerebral cortical neuronal morphology has been particularly well documented in analyses of Golgi-stained tissue from experimental animals exposed to alcohol during the fetal period (40–43) and in tissue from individuals with Rett syndrome (44) (as well as in MECP2-deficient mice (45), a genetic model of Rett syndrome). Given the potential relationship between cortical FA and morphological differentiation of the neuropil, it is possible that DTI measurements could be used to detect anatomical abnormalities within a class of neurodevelopmental disorders.
Current strategies that utilize DTI to characterize the neurobiological basis of several neurodevelopmental disorders have mostly focused on cerebral white matter (WM) of affected individuals at maturity or stages of development subsequent to the loss of cortical FA. Reduced WM FA relative to controls has been reported within contexts of disorders with genetic (e.g., Rett syndrome (46, 47), phenylketonuria (48)), environmental (e.g., fetal alcohol spectrum disorder (49–52), premature birth (53, 54)), or multifactorial (e.g., autism (55), schizophrenia (56–58)) origins. It is known that plasticity in the CNS decreases after critical/sensitive periods which end prior to the completion of myelination within brain WM (59–61). These critical periods are specific periods of time, during which particular functional systems can be formed. Abnormal development of, or coordination among, multiple neural components (i.e., neurons, dendrites, axons, synapses, sensory afferents) during this time could lead to abnormal maturation and permanent dysfunction. For example, deprivation of visual sensory experience early in brain development has been demonstrated to produce permanent effects on visual system processing (61–63). Thus, a DTI-based approach aimed at detecting morphological characteristics of disease within the developing cerebral cortex could potentially provide a new strategy that would extend the capabilities of DTI toward identification of anatomical abnormalities prior to the end of these critical developmental periods.
3 Methods for Quantifying Changes in Cortical FA with Brain Development
An objective of this review is to determine whether the high-to-low change in cortical FA with age for a given species occurs at a rate that would be predicted based on other comparative studies of brain development. In order to make such a comparison, cortical FA measurements reported by several laboratories, using a variety of experimental approaches, must be combined. It is therefore important to recognize methodological differences between the DTI experiments reviewed here so that potential sources of differences between studies may be appreciated. The following discussion summarizes the primary factors that lead to inter-laboratory differences in cortical FA values. As can be observed in Fig. 13.2, differences in the magnitude of FA values exist between studies. However, an underlying assumption of the analysis presented here is that the rate of change in FA within each of the studies reviewed is, neglecting species-specific differences, consistent between studies despite differences in absolute FA values at a given age. Justification of this approximation is based on acknowledgment that experimental conditions are held fixed within each of the studies shown in Table 13.1 with respect to the factors discussed below.
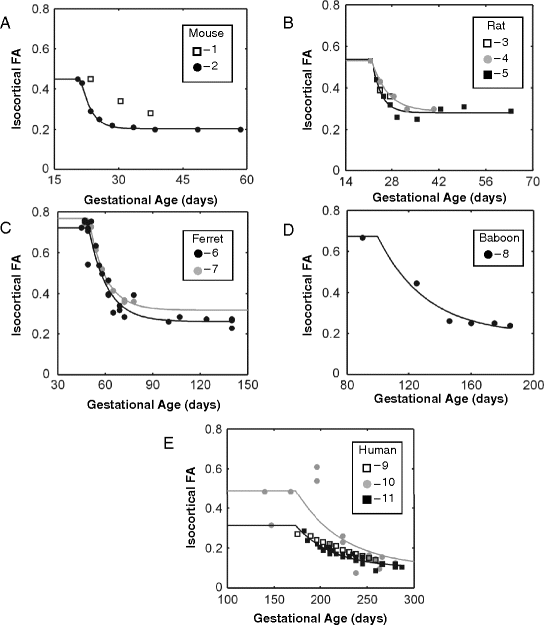

Fig. 13.2.
Isocortical fractional anisotropy is plotted as a function of post-conceptional age in five different species. Data from 11 independent studies were fit to the empirical mathematical model expressed in Equation [5]. Fractional anisotropy across species shows an exponential decline with development over the age ranges pictured. Data in a–e are pictured for mouse, rat, ferret, baboon, and human species, respectively. Squares indicate data collected in vivo, while circles represent data collected from post-mortem samples. Open shapes indicate data that were insufficient for modeling a time constant for an exponential decline in FA (τ FA); 1 = (89), 2 = (92), 3 = (29), 4 = (28), 5 = (75), 6 = (34), 7 = (93), 8 = (27), 9 = (37), 10 = (10), 11 = (76).
Table 13.1
Summary of DTI parameters and methodology employed in the reviewed articles
Species | Mouse | Rat | Ferret | Baboon | Human | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
References | (92) | (89) | (29) | (75) | (28) | (93) | (34) | (27) | (10) | (76) | (37) |
Tissue | Ex vivo | In vivo | In vivo | In vivo | Ex vivo | Ex vivo | Ex vivo | Ex vivo | In vivo | Ex vivo | In vivo |
Measure | FA | FA | FA | FA | FA | RA | FA | RA | A σ | FA | FA |
N/point | ∼4 | 13–16 | Unknown | ∼5 | 2 | 1–3 | 1–2 | 1–3 | 24 total | 4–12 | 37 total |
Time points (post-conceptional age) | 20–59 | 23–73 | 24–28 | 21–64 | 21–41 | 45–140 | 47–241 | 90–185 | 182–287 | 140–371 | 175–266 |
Magnetic field strength (T) | 9.4 | 9.4 | 4.7 | 7.0 | 9.4 | 4.7 | 4.7/11.7 | 4.7 | 1.5 | 1.5 | 1.5 |
Image resolution (RO/PE/slice) (mm)a | ≤.125 ×.125 ×.125 | .2 ×.2 ×.5 | .125 ×.125 ×.5 | .27 ×.27 ×.5 | ≤.14 ×.14 ×.14 | ≤.35 ×.35 ×.35 | ≤.35 ×.35 ×.35 | ≤.5 ×.5 ×.5 | 1.9 ×1.9 ×5 | ≤.94 ×.94 ×3 | 1.4 ×1.4 ×3 |
TE (ms) | 34 | 23.3 | 40 | 38 | 34 | 67 | 42–67 | 67 | 106 | 100 | 99.5 |
TR (ms) | 800 | 2,000 | 1,500 | 4000 | 700 | 3,400–5,800 | 4,000–10,500 | 3,450–4,000 | 3,000 | 8,000 | 7,000 |
No. of dir. | 6 | 6 | 6 | 21 | 6 | 25 | 22/25 | 25 | 7 | 10 | 6 |
b value (s/mm2) | 1,758 | ∼700 | 763 | 700 | 1,000 | 200–12,100 | 200–2,500 | 500–12,500 | 340–800 | 700 | 600 |
ROI location (or surface analysis) | L,R; mid-coronal | Mid-sagittal | Parietal cortex | L,R; mid-coronal | Assigned to functional cortical areas | Lateral to caudate nucleus | Surface | Surface | Parietal, occipital cortices | Parietal, occipital, frontal, temporal cortices | Precentral, post-central, sup. frontal, sup. occipital gyri |
3.1 DTI Measurements Have Been Performed on a Diverse Array of Experimental Subjects
3.1.1 In Vivo Versus Post-mortem
The use of post-mortem tissue permits long scanning times for imaging experiments, which can be used to obtain high-image spatial resolution with a high signal-to-noise ratio (SNR). As a result, MRI investigations of the CNS utilizing post-mortem tissue have seen increasing use over recent years (19, 26–28, 34, 64–71), and much progress has been made toward understanding the degree of correspondence between in vivo and ex vivo measurements (64, 65, 67, 70–74). Due to the sensitivity improvements that can be realized, many of the investigations of cortical FA changes with development listed in Table 13.1 have been performed on post-mortem tissue.
One difference in water diffusion between in vivo and post-mortem tissue is that the apparent diffusion coefficient (ADC) of water decreases by a factor of ∼2.7 (71) following death and tissue perfusion fixation. This decrease in the ADC likely arises from several differences between living and post-mortem tissue, including physiological (e.g., membrane permeability to water) and temperature (magnet bore vs. physiological temperature) variations (64, 65, 72, 73). A practical consequence of the low ADC value in post-mortem tissue is a requisite pulsed-field gradient system capable of producing strong (approximately 20 G/cm or greater) magnetic field gradients to achieve appropriate diffusion-sensitization settings (“b values”) to characterize water diffusion without requiring excessively large echo time (TE) values. Such gradient capabilities are standard on small animal imaging MRI systems but are not included in human clinical instrumentation.
In spite of the large difference in ADC between living and post-mortem tissue, diffusion anisotropy differences between the two tissue states in adult GM and WM structures have been found to be less significant (64, 65, 72, 73) if present at all (67, 71). Specifically, within the context of the developing cerebral cortex, time courses of cortical FA changes with development in rat in vivo (29, 75) and post-mortem (28) are highly similar, as are comparisons between post-mortem human (68) or non-human (27) primates and in vivo human studies (10, 11, 37). The analysis presented below provides further evidence that similar conclusions with regard to development of the cerebral cortex can be drawn from in vivo and post-mortem DTI measurements.
With regard to comparisons between measurements performed on living and post-mortem tissue, an additional layer of complexity is introduced in studies of post-mortem tissue that has not undergone fixation with aldehydes. Empirical data show that FA measurements obtained from post-mortem brain tissue vary with the amount of time that elapses between death and tissue fixation due to autolysis (64, 72). An implication of this finding is that measurements conducted on unfixed post-mortem tissue will depend on the post-mortem interval prior to data collection. For obvious reasons, this aspect of a DTI study of human subjects is not readily controlled (76, 77).
3.1.2 Measurements in Species with Gyrencephalic Versus Lissencephalic Brains
One striking difference between cerebral cortices of lower (mouse, rat) and higher (ferret, old world monkey, human) animal forms studied by DTI is the presence of sulcal and gyral fissures on the latter at maturity. Notably, the cerebral cortices of gyrencephalic species do not posses gyri and sulci at the developmental stage immediately following migration of pyramidal neurons to the cortex. The loss of cortical FA with development coincides with cortical folding in these species. Therefore, the question arises whether mechanical forces associated with cortical folding influence cortical FA measurements exclusively within gyrencephalic species and thus confound comparisons with rodents. The analysis below demonstrates that, despite significant differences in the extent of cortical folding between species, cortical FA changes occur over a remarkably consistent period of brain development. Further, the potential role of gyrus/sulcus formation on the loss of cortical FA was specifically investigated in a study of ferret brain development (34). It was observed that cortical FA was slightly larger within sulci than gyri at a given age, but that variation throughout the cortical sheet in FA due to position relative to gyri/sulci was modest relative to temporal, laminar, and regional patterns in FA (34).
3.2 DTI Measurements Have Been Performed Using Varying Experimental Settings
3.2.1 Image Resolution
In the studies summarized in Table 13.1, a range of image resolution settings were used for measuring diffusion anisotropy. As a result of variation in the thickness of the cerebral cortical wall with brain volume among species, the laminar gradient in cortical FA is usually expressed over a different distance scale for different species. Comparative studies of the dependence of mean cortical thickness upon cortical volume (78, 79) lead to estimates that rat cerebral cortex (mean cortical thickness = 1.05 mm) is 39% of that of human (2.72 mm). Given these dimensions, it should be recognized that cortical FA values typically reflect averaged morphological tissue properties over multiple cortical lamina. This is particularly true in the developing cerebral cortex, which is thinner than the cortex at maturity.
3.2.2 Number of Diffusion-Sensitization Directions
In DTI studies directed at WM, it has become recognized that water diffusion within volume elements that overlap multiple fiber tracts of different orientations can give rise to multimodal diffusion tensors (80). In order to infer complex WM fiber architecture, it is necessary to make use of measurement schemes in which several (e.g., 25 or more) diffusion-sensitization directions are sampled. Image acquisition procedures such as high-angular resolution diffusion imaging (81, 82), diffusion spectrum imaging (83), or q-ball (84) can be used to facilitate such sophisticated DTI analyses. In contrast to the multimodal fiber orientation distribution expected within some regions of WM, reports on the distribution of axonal and dendrite orientations inferred from DTI measurements of the developing cerebral cortex to date have revealed unimodal (85), radially oriented axial symmetry. The corresponding axial symmetry observed for water diffusion within the immature cerebral cortex enables data to be modeled with a less complex DTI expression than that typically used for WM (26, 85). Therefore, analyses of cortical diffusion anisotropy have, in many cases, made use of a modest number (less than 12) of diffusion-sensitization directions. Generally, however, in DTI investigations, the SNR increases with the amount of time devoted to acquiring data, and thus studies with additional diffusion-sensitization directions gain precision relative to DTI measurements that sample a coarser set of directions over a shorter period of time.
3.3 Multiple Post-acquisition Analyses Have Been Employed to Quantify Diffusion Anisotropy
In order to perform a quantitative analysis of cortical FA changes with age, a reliable method of extracting FA values from MRI data is needed. Specifically, it is important that an approach adopted to quantify cortical FA avoids potential covariation due to dependencies on laminar and regional position. A number of strategies have been described for accomplishing this. The array of analysis procedures may be broadly categorized into region of interest (ROI) and surface-based methods.
3.3.1 ROI Analyses
In the majority of studies summarized in Table 13.1, cortical FA is quantified within a number of individuals through manual delineation of a region of the cerebral cortex and reporting an average within the identified region. Such an approach can be used to produce highly reliable estimates of cortical FA because manual supervision can ensure that consistent regions are delineated across individuals and can verify the location of the ROI boundaries with respect to regional and laminar position. One drawback, however, is that ROI dimensions are large relative to individual cortical lamina and therefore averaged FA values include contributions from cortical tissue that has undergone varying extents of morphological differentiation. Lastly, due to the need for a rater to prescribe the location of ROI boundaries, this technique is susceptible to rater-induced bias.
Huang et al. (28) have described an ROI-based approach that addresses cortical FA variation due to laminar position. For each region-specific ROI, these investigators quantified FA within three zones defined relative to distance from the pial surface along a line normal to the local surface tangent plane. Laminar specificity is thus obtained from the authors’ reports of cortical FA changes with age in outer, medial, and inner cortical zones (28).
3.3.2 Surface-Based Methods
An approach that can be used to address regional and laminar patterns in cortical FA utilizes surface models of the cortical sheet (86). For visualization purposes, Huang et al. (28) projected cortical FA values onto a cortical surface model by color-coding the model according to the FA within the voxel intersected by the surface. By incorporating surface registration procedures (86), it is possible to delineate the boundaries of an ROI on an atlas surface (to produce a “surface-based ROI” rather than a “volume-based ROI” as described above) and automatically project the ROI boundaries on surface models representing individual brains in order to facilitate quantitative analyses of cortical FA values. This approach was adopted in a study of baboon development (27). Surface-based methods also can facilitate an analysis that accommodates laminar variation in cortical FA. As an example, an approach similar to Huang et al. (28) was adopted in a study of ferret development, in which line segments normal to the local surface tangent plane were defined for every node on each animal’s surface (34). To extract cortical FA values specifically from the immature superficial lamina of the developing cortex, the maximum cortical FA value intersected by each line segment was projected onto the surface models. Thus, surface-based methods can be used to generate automated analyses that account for potential variation in cortical FA values due to laminar and regional heterogeneities in temporal patterns of morphological differentiation.
< div class='tao-gold-member'>
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


