Practical Calculations

Learning Objectives

After studying this chapter, you should be able to

1. Exhibit an understanding of the systems of measurement.

2. Explain how to perform conversions while using the metric system and other systems of measurement.

3. Demonstrate how to perform dosage calculations.

4. Explain how percent concentrations are prepared.

Key Terms

Dosage rate

Dose

Equivalent weight

Milliequivalent

Percent concentration

Ratio concentration

Solution

Stock solution

Introduction

Veterinary technicians often are asked to prepare and administer medications to animal patients. A veterinarian’s orders may ask for administration of a specific number of milligrams or units of medication (dose). The technician then must determine the quantity (e.g., in milliliters or tablets) of the preparation that contains the appropriate dose. In other instances, the technician may be asked to calculate the dose on the basis of a dosage rate (found in the insert or in reference books) and the animal’s weight. In either case, an error in calculation can seriously affect the health of a patient. This chapter provides the background information and applications needed by the veterinary technician to accurately carry out a veterinarian’s medication orders.

Mathematic Fundamentals

It is assumed that the student who uses this text has a basic understanding of fractions and decimals. With these fundamentals as a background, the concepts of percent, ratio, and proportion should be reviewed before the practice problems are solved.

Percent is defined as parts per hundred. Percent is a fraction with the percent as the numerator and 100 the denominator (e.g., 5% = 5/100). Percents may be written as decimals, fractions, or whole numbers.

Example 1: Decimal: 0.3%

(three-tenths percent [3/10 ÷ 100])

Fraction: 1/5%

(one-fifth percent [1/5 ÷ 100])

Whole number: 5%

(five percent [5 ÷ 100])

Percent may be changed to fractions or decimals.

Example 2: Change to a fraction:

5%=5/100=1/20

Change to a decimal:

5%=5/100=0.05

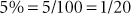
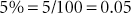
Note that a percent can be changed to a decimal quickly by dropping the percent sign and moving the decimal two places to the left.

Example 3:

5%=0.05

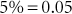
A ratio is a way of expressing the relationship of a number, quantity, substance, or degree between two components. In reality, ratios are fractions, with the first number in the ratio the numerator and the second number the denominator. The numbers may be placed side by side, separated by a colon, or they may be set up as a numerator/denominator (e.g., 1 : 5, 1/5). In mathematics, a ratio may be expressed as a quotient, a fraction, or a decimal, per the following:

Example 4:

1÷5, 1/5, 51.0=0.2

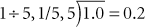
A proportion shows the relationship between two ratios. When a proportion is set up, the two ratios usually are separated by an = (equals) sign.

Example 5:

8:16 as 1:2 or 816=12

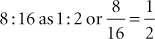
The proportions above read “8 is to 16 as 1 is to 2.” The two inner numbers in the first example (16 and 1) are called the means, and the two outer numbers (8 and 2) are called the extremes. In a true proportion, the product of the means equals the product of the extremes (16 × 1 = 16; 8 × 2 = 16). This fact makes the proportion a useful mathematical tool. When a part of the problem is unknown, X can be substituted for the unknown part in the proportion and the equation solved for X. Care must be taken to ensure that the proportion is set up correctly, and that the same unit of measure is used on both sides of the equation.

Example 6:

8:16=1:X or 816=1X8X=16X=2

Example 7: To convert 0.2 g to milligrams, calculate the following:

1000 mg:1 g=X mg:0.2 g or 1000 mg1g=X mg0.2gX=200(1000×0.2)

Systems of Measurement

The first step in the successful calculation of doses is to develop an understanding of the units of measure used to carry out the calculations. These units are components of the following three separate systems:

1. Metric system

2. Apothecary system

3. Household system

All three systems are expressed in the fundamental units of weight, volume, and length. Technicians should be able to convert values within each system and between the three systems.

Metric System

The fundamental units of measurement in the metric system are the gram (weight), the liter (volume), and the meter (length). Gram is abbreviated g or gm, liter is abbreviated L or l, and meter is abbreviated m. The usefulness of the metric system is that all units are powers of the fundamental units. Prefixes are used in combination with fundamental units to denote smaller or larger quantities. Table 3-1 illustrates the units of measurement used in the biologic sciences.

TABLE 3-1

Units of Measure for the Biologic Sciences

WEIGHT	VOLUME	LENGTH	MULTIPLE POWER OF 10
Gram (g)	Liter (L)	Meter (m)	1
Kilogram (kg)	Kiloliter (kL)	Kilometer (km)	1000
Decigram (dg)	Deciliter (dL)	Decimeter (dm)	1/10
Centigram (cg)	Centiliter (cL)	Centimeter (cm)	1/100
Milligram (mg)	Milliliter (mL)	Millimeter (mm)	1/1000
Microgram (µg)	Microliter (µL)	Micrometer (µm)	1/1,000,000
Nanogram (ng)	Nanoliter (nL)	Nanometer (nm)	1/1,000,000,000
Picogram (pg)	Picoliter (pL)	Picometer (pm)	1/1,000,000,000,000

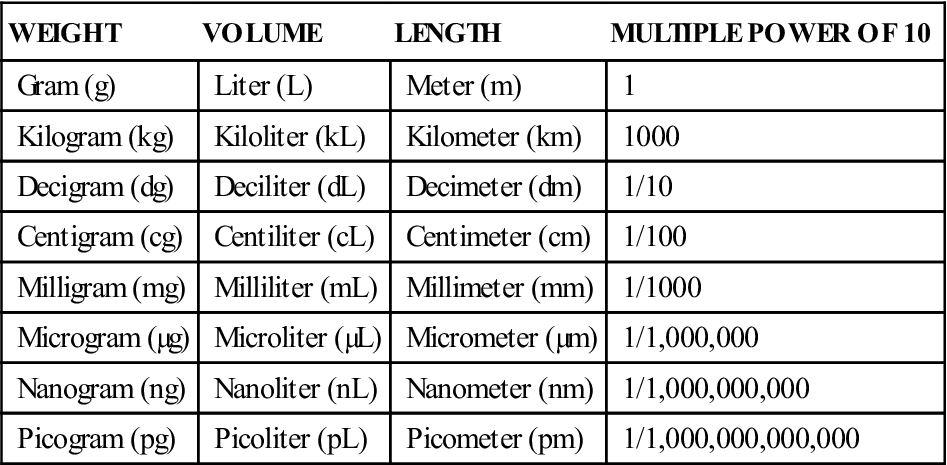
The units that are used most commonly in dosage calculations include the gram, the kilogram (kg; 1000 g), the milligram (mg; 1/1000 g), and the milliliter (mL; 1/1000 L). It should be noted that a milliliter is equivalent to the quantity of water contained in 1 cubic centimeter (cc), which is also equivalent to 1 g of weight. Therefore, for practical purposes, it may be said that 1 mL = 1 cc = 1 g.

On occasion, the microgram (µg) may be used. (It should be noted that this unit also may be abbreviated as mcg.) Care should be taken to differentiate this abbreviation from mg, which looks very similar when written orders are used.

Conversion Between Metric Units

The most fundamental way to convert between metric units is to multiply the units given by the conversion factor involving the units desired. If the desired conversion is from milligrams (mg) to grams (g), the number of milligrams given should be multiplied by the factor 1 g/1000 mg because 1 g = 1000 mg. The following steps would be involved in this conversion:

1. Write down the number of milligrams to be converted to grams.

2. To the right of that number, write down the number of milligrams in 1 g, with the milligrams as the denominator. (The numerator should always contain the unit to which you wish to convert.)

3. Multiply the two numbers together.

Example 1: Convert 3000 mg to grams.

Step 1.Step 2.Step 3. 3000 mg3000 mg 1g1000 mg3000 mg×1g1000 mg=3 g

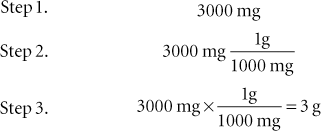
Figure 3-1 illustrates the stairstep method of converting from one unit to another within the metric system. When converting measurements in the metric system via the stairstep method, divide by 10 for each step up to the desired measurement, and multiply by 10 for each step down to the desired measurement.
You also may think of converting measurements with this method by remembering that for each step up, the decimal point is moved one place to the left. For each step down, the decimal point is moved one place to the right.

Example 2:

500 mL=_____ L

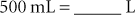
Conversion of milliliters to liters requires three steps upward. Therefore, divide 500 by 10 three times (or 500 ÷ 1000). This moves the decimal point three places to the left, and the answer is 500 mL = 0.5 L.

Example 3:

2 g=_____ mg

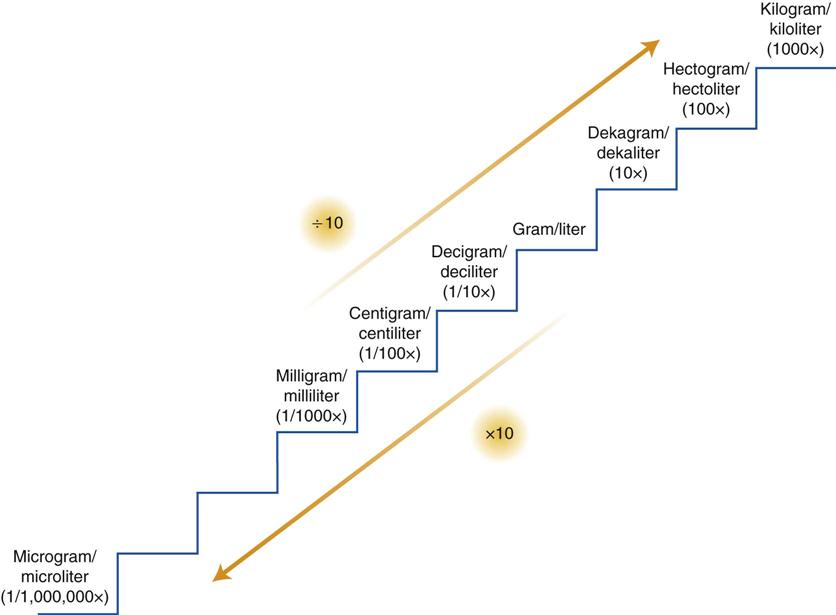
To convert grams to milligrams, go down three steps. Multiply 2 by 10 three times (or 2 × 1000). This moves the decimal point three places to the right, and the answer is 2 g = 2000 mg.

A second method for performing conversions in the metric system can be called the arrow method. When this method is used, it is paramount to remember which units of measure are larger. Conversions between the commonly used units of kilograms, grams, milligrams, and micrograms are illustrated in the following text.

A kilogram is 1000 times larger than a gram (g), a gram is 1000 times larger than a milligram (mg), and a milligram is 1000 times larger than a microgram (mcg). This relationship can be abbreviated as follows with the use of the “greater than” symbol (>):

kg>g>mg>mcg

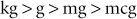
Many times, the technician will have to calculate the amount of drug to be given when the supply on hand is not measured in the same units as the order calls for. For example, the order is for 0.3 g of drug A, and the supply on hand is 150-mg tablets. Before it can be determined how many tablets should be given, 0.3 g must be converted to milligrams. Because it is known that 1 g = 1000 mg, 0.3 g can be changed to milligrams by multiplying 0.3 g by 1000 mg/g (0.3 × 1000 = 300 mg). The decimal point is moved three places to the right (0.3 → 3_↑1 0_↑2 0_↑3).

The conversion could have been made very quickly by simply moving the decimal point three places to the right. To know which direction to move the decimal, one should determine which way the arrow is pointing (e.g., kg > g > mg > mcg).

Any time the conversion is made between two adjacent units in the relationship of kg > g > mg > mcg, the decimal point will be moved three places.

The steps for converting grams to milligrams with the use of this method are as follows:

1. Write down the order first, using the units called for (0.3 g).

2. Write down the equivalent units (on hand) needed next to the order units (0.3 g = __ mg).

3. Place an arrow between the two units, with the closed part of the arrow pointing toward the smaller unit (g > mg)

4. Move the decimal point three places in the direction the arrow points (0.3 g → 3_↑1 0_↑2 0_↑3).

In the previous problem, it would take two 150-mg tablets to fill the 300-mg order.

If the order had been for 300,000 mcg of drug A, and the supply on hand had consisted of 150-mg tablets, micrograms would have to be converted to milligrams through the following steps:

1. Write the order (300,000 mcg).

2. Write down the equivalent units needed next to the order units (300,000 mcg = ___ mg).

3. Place an arrow between the two units, with the closed part of the arrow pointing toward the smaller units (mcg < mg).

4. Move the decimal three places in the direction the arrow points (300 mg ← 300_↑3 0_↑2 0_↑1 0. mcg).

In this problem, it would take two 150-mg (150,000 mcg) tablets to fill the 300,000-mcg order.

Additional problems for converting within the metric system are provided at the end of this chapter.

Apothecary and Household Systems

The apothecary and household systems of measurement are older systems than the metric system. The apothecary system is seldom used, but the household system is used for giving clients instructions about dosage.

The units most often encountered in the apothecary system are the minim, abbreviated m or min; the dram, abbreviated dr; the ounce, abbreviated oz; and the grain, abbreviated gr. A minim is equal to 1 drop, a dram is equal to 4 mL, an ounce is equal to 30 mL, and a grain is equal to 65 mg (64.8, sometimes rounded to 65). When quantities related to grains are written, the symbol gr should be placed before the number, and common fractions are used when appropriate (e.g., gr 1/50). The apothecary pound (12 oz) is not used when doses are calculated. Instead, the avoirdupois pound (16 oz) is used.

Units commonly used in the household system include the drop, abbreviated gtt; the tablespoon, abbreviated T or Tbsp; and the teaspoon, abbreviated t or tsp. One drop is equivalent to 1 min, 1 Tbsp is equivalent to 15 mL, and 1 tsp is equivalent to 5 mL. The pint, quart, and gallon are other units that are sometimes encountered. Boxes 3-1 and 3-2 illustrate equivalent values that are useful in dosage calculations. Practice problems for converting within and between the apothecary and household systems are found at the end of this chapter.

Box 3-1

Weight Equivalents

1 kg = 1000 g = 2.2 lb

1 g = 1000 mg

1 mg = 1000 µg = 0.001 g

65 mg = 1 gr

1 µg = 0.001 mg = 0.000001 g

1 lb = 453.6 g = 0.4536 kg = 16 oz

1 oz = 28.35 g

Box 3-2

Volume Equivalents

1 L = 1000 mL = 1 qt (946.4 mL)

500 mL = 1 pt (473 mL) = 2 cups (equivalent to 1 lb of water)

Dosage Calculations

The quantity of drug to be delivered to a patient is called the dose. A dosage rate expressed in milligrams per kilogram (or milligrams per pound) is multiplied by the animal’s weight in kilograms (or pounds) to determine the dose. The dose then is divided by the amount (concentration) of the drug in the pharmaceutic form (e.g., tablet or solution) to determine the actual amount of the pharmaceutic form to be administered. The formula for dosage calculation, which should be committed to memory, is as follows:

Dose=Animal′s weight×dosage rateConcentration of drug

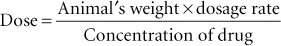
Example 1: If a 20-kg dog is to be given amoxicillin at the rate of 10 mg/kg and injectable amoxicillin at a concentration of 100 mg/mL is available, the dosage calculation would be as follows:

Dose=20 kg×10 mg/kg100 mg/mL=200 mg100 mg/mL=2 mL

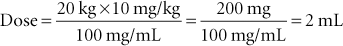
Note that in the first step of the calculation, kilograms cancel out and leave only milligrams in the numerator. In the second step, milligrams cancel out and leave milliliters. If 100-mg amoxicillin tablets are available, the formula becomes as follows:

Dose=20 kg×10 mg/kg100 mg/tablet=200 mg100 mg/tablet=2 tablets

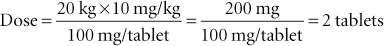
Because most scales used to weigh animals for drug dosage calculation provide the weight in pounds, a conversion must be made from pounds to kilograms. To do this, divide the weight in pounds by 2.2.

Example 2: The dog in the previous problem weighed 44 lb, and 44 divided by 2.2 equals 20 kg. To convert kilograms to pounds (if the dose is provided in milligrams per pound), multiply the weight in kilograms by 2.2 (e.g., 20 kg × 2.2 = 44 lb).
If the order to the technician is to “give a dog 300 mg of amoxicillin,” then the ordered amount is simply divided by the concentration of the drug to determine the amount to be administered.

Example 3: If the order is to give a dog 300 mg of amoxicillin (concentration 100 mg/mL), the calculation would be as follows:

300 mg100 mg/mL=3 mL

Technician Notes

Because drugs are manufactured in different concentrations, always record the dose (milligrams, units, mEq) of active ingredient in the medical record rather than the number of milliliters, tablets, etc.

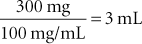
It should be noted that the dose of most drugs used to treat neoplasms is calculated according to the total body surface area of the patient. Body surface area is correlated with the weight of the animal. A table is available in Chapter 16 (see Table 16-2) for converting an animal’s weight to surface area in square meters (sq M or m²). In these cases, the formula for dosage calculation becomes the following:

Dose=mg/m2(from insert)×m2(from table)

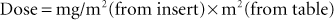
Dosage calculation problems are provided at the end of this chapter.

Solutions

To understand dosage calculation problems and how to prepare dilutions of substances (e.g., allergy injections and disinfectants), a technician must have a basic understanding of solutions. Solutions are mixtures of substances that usually are not chemically combined with each other. In most cases the solvent will be a liquid, but it can be a solid. Solutions are made up of a dissolving substance, called the solvent, and a dissolved substance, called the solute. Not all substances form solutions with each other. Those that form solutions are called miscible, and those that do not are called immiscible. A solution is referred to as saturated if it contains the maximum amount of solute at a particular temperature and pressure. Under some circumstances, a solution can become supersaturated. Mixtures of substances in which the solute is made up of very large particles are called suspensions. The particles in suspensions settle on standing, and the mixture must be agitated before it is administered. True solutions do not settle and remain mixed without agitation. All parts of solutions contain equal parts of the solute.

When working with solutions, it is important to know the amount of solute in the solvent or to be able to measure it. The amount of solute dissolved in the solvent is referred to as the concentration (strength) of the substance. Concentrations may be expressed in a number of ways, including the following: