Chapter 3
An introduction to pharmacokinetics
Tension (partial pressure), units and atmospheric pressure
Solubility coefficients of gases
Blood solubility and alveolar tension
The tension of anaesthetic agents in brain tissue
Speed of uptake and elimination related to safety of inhalation agents
Uptake and elimination of inhalation anaesthetics in clinical practice
Other factors affecting inhalation anaesthetic administration
Total apparent volume of distribution
Total elimination clearance (ClE) and elimination half-life (t1/2β)
Practical methods of drug delivery during intravenous anaesthesia
Introduction
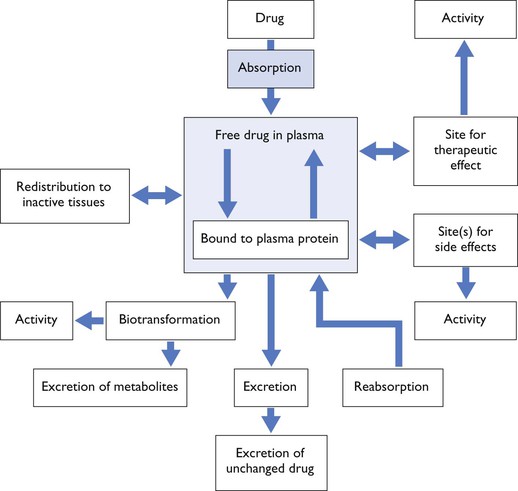
The term pharmacodynamics refers to the relationship between drug concentration and its clinical or pharmacological effect, while pharmacokinetics refers to the mathematical description of the various processes relating to drug movement from the site of its administration, followed by distribution to the tissues and, finally, elimination from the body. To paraphrase, pharmacokinetics is ‘what the body does to the drug’ whereas pharmacodynamics is ‘what the drug does to the body’. However, they cannot be regarded as separate processes for drugs produce effects in vivo which alter their own kinetic and dynamic profiles, for example acute haemodynamic effects will influence distribution (Fig. 3.1).
Physical principles
In the account of the pharmacokinetics of inhaled drugs that follows, frequent reference is made to tensions, solubilities and concentrations of gases in solution. These terms may perhaps be best explained by considering specific examples.
Tension (partial pressure), units and atmospheric pressure
The tension of a gas in a liquid is the pressure of the agent in the gas with which the liquid should be in equilibrium. A liquid and a gas, or two liquids, are in equilibrium if, when separated by a permeable membrane, there is no exchange between them. The statement that ‘the tension of nitrous oxide in the blood is 50.5 kPa (380 mmHg)’ means that if a sample of blood were placed in an ambient atmosphere containing nitrous oxide at a concentration of 50% v/v (and, therefore according to Dalton’s law, exerting a partial pressure of 50.5 kPa (380 mmHg), there would be no movement of nitrous oxide into or out of the blood. ‘Tension’ is a term used by physiologists and anaesthetists, while physicists speak of ‘partial pressure’.
In the example above, tensions (partial pressures) are given in two units, mmHg, but also in kilopascals (kPa) which is the SI unit and which, as veterinary scientists, we should be using. Reluctance to change is partly due to the fact that atmospheric pressure in weather forecasts is presented in a variety of different units depending on the country. For many years, atmospheric pressure was given to us in mmHg (before that in inches Hg). In Europe, SI units are used, and atmospheric pressure is presented as millibars. A millibar is, in fact, a hectopascal, so 10 millibars = 1 kPa. ‘Standard’ atmospheric pressure at sea level is approximately 760 mmHg or 1013 millibars (101.3 kPa).
With an inhalation anaesthetic, anaesthesia depends on the tension (partial pressure) of the agent. Minimum alveolar concentration (MAC, see Chapter 1) is expressed as volume %. For example, if at sea level MAC was 1%, a tension of 1% of standard atmospheric, i.e. 7.6 mmHg or 1.01 kPa is what is required to prevent movement in response to stimulation in 50% of animals. However, if anaesthesia is carried out at an elevation of 2000 metres, atmospheric pressure is approximately 80 kPa, so the % of anaesthetic gas required to give a tension of 1.01 kPa is now 1.25 %. Thus, MAC expressed as vol% has to be corrected for the atmospheric pressure (Mapleson, 1996). Fortunately, in clinical practice, most calibrated vaporizers are compensated such that, at any dial setting, they put out a specific partial pressure of the agent, even although the dial says % (see Chapter 10) and so the anaesthetist may not realize that they are administering a higher % (but the same mass) of anaesthetic.
Solubility coefficients of gases
At any given temperature, the mass of a gas dissolved in a solution, i.e. its concentration in the solution, varies directly with its tension (Henry’s law) and is governed by the solubility of the gas in the particular solvent. The solubility of anaesthetics varies widely and, therefore, at any one tension, the quantities of the different anaesthetics in the solvent are not equal. The solubility of anaesthetics in the blood and tissues are best expressed in terms of their partition, or distribution, coefficients. For example, the blood–gas partition coefficient of nitrous oxide is 0.47. This means that when blood and alveolar air containing nitrous oxide at a given tension are in equilibrium, there will be 47 parts of nitrous oxide per unit volume (say per litre) of blood for every 100 parts of nitrous oxide per unit volume (litre) of alveolar air. In general, the partition coefficient of a gas at a stated temperature is the ratio, at equilibrium, of the gas’s concentration on the two sides of a diffusing membrane or interface.
Tissue solubility does not necessarily correlate with blood–gas solubility. The newer volatile agents (e.g. isoflurane, desflurane, sevoflurane) may have a low blood–gas partition coefficient but their brain–blood partition coefficient is not necessarily lowered to the same extent. The brain–blood partition coefficient can be estimated by dividing the brain–gas with the blood–gas partition coefficient. The brain–blood partition coefficients for halothane, enflurane, isoflurane and desflurane calculate to be 1.86, 1.73, 1.67 and 1.27, respectively. Hence desflurane has a more rapid uptake in the brain tissue. For simplicity, in many theoretical calculations, it is often assumed that in the brain and all other tissues (except fat) gases have very nearly the same solubility as they have in blood because their tissue–blood partition coefficients are sufficiently close to unity.
Concentration of a gas in solution
The concentration of a gas in solution may be expressed in a variety of ways including:
Pharmacokinetics of inhaled anaesthetics
Inhaled anaesthetics have a pharmacokinetic profile which results in ease in controlling the depth of anaesthesia as a result of rapid uptake and elimination: a knowledge of this profile can facilitate their use in clinical practice. They cannot be introduced into the brain without at the same time being distributed through the entire body, and this distribution exerts a controlling influence over the rate of the uptake or elimination of the anaesthetic by brain tissue. Even if the inhalation agent is metabolized to a considerable extent (e.g. halothane), such metabolism does not play a clinically significant part in removal of the anaesthetic. Thus, all inhalation anaesthetics may be regarded as essentially inert gases as far as uptake and elimination are concerned.
Uptake of inhaled anaesthetics
If some factors are reduced to their simplest possible terms, and certain assumptions are made, it is possible to give approximate predictions relating to inert gas exchange in the body (Bourne, 1964). These predictions are sufficiently realistic for practical purposes and serve to illustrate the main principles involved. Once these are understood more elaborate expositions found elsewhere (Eger, 1974; 2010; Mapleson, 1989) should become reasonably easy to follow.
For simplicity, the physiological variables such as cardiac output and tidal volume must be assumed to be unaffected by the presence of the gas, and to remain uniform throughout the administration. Allowance cannot be made for alterations in the tidal volume as administration proceeds. The blood supply to the grey matter of the brain must be assumed to be uniform and the gas to be evenly distributed throughout the grey matter. Finally, although in practice anaesthetics are seldom administered in this way, the anaesthetic must be assumed to be given at a fixed inspired concentration, and, what is more, it must be assumed that no rebreathing of gases occurs.
The tensions of the gas in the alveolar blood and tissues all tend to move towards inspired tension (Kety, 1951), but a number of processes, each of which proceeds at its own rate, intervene to delay the eventual saturation of the tissues. The tension of the gas in the brain follows, with a slight delay, its tension in the alveolar air. Since both the rate of induction and recovery from inhalation anaesthesia are governed by the rate of change of the tension of the anaesthetic in the brain, and this in turn is governed by the rate of change of tension in the alveoli, the factors that determine the anaesthetic tension in the alveoli are obviously of very great importance.
The rate at which the tension of an anaesthetic in the alveolar air approaches its tension in the inspired air depends on the pulmonary ventilation, the uptake of the anaesthetic by the blood and tissues, and the inspired concentration. First, by means of pulmonary ventilation the gas is inhaled, diluted with functional residual air, and enters the alveoli. This is where diffusion occurs and normally the alveolar gas equilibrates almost immediately with the pulmonary blood, which is then distributed throughout the body. A second diffusion process occurs across the capillary membranes of the tissues into the interstitial fluid and from there through the cell membranes into the cells themselves. Venous blood leaving the tissues is in equilibrium with the tissue tension. The blood from the tissues returns to the lungs, still carrying some of its original content of anaesthetic, and is again equilibrated with alveolar gas which now contains a slightly higher tension of the anaesthetic. It is in this manner that the alveolar (or arterial) and venous (or tissue) tensions of the anaesthetic in question gradually, and in that order, rise towards eventual equilibrium with the inspired tension.
As this complex process proceeds, the tension of the anaesthetic in the alveolar air increases continuously, but not at a uniform rate. Plotted against time, alveolar tension rises in a curve that is, in general, the same for every inert gas (Fig. 3.2). This curve tails off and slopes gradually upwards until, after several hours or even days, depending on the anaesthetic in question, complete equilibrium is reached. The steep initial rise represents movement of anaesthetic into the lungs, i.e. the pulmonary wash-in phase. The slowly rising tail represents more gradual tissue saturation. The change from steep part of the curve to the tail marks the point at which lung wash-in gives place to tissue saturation as the most important influence. The tail can be very long if the anaesthetic in question has a very high fat/blood partition coefficient.
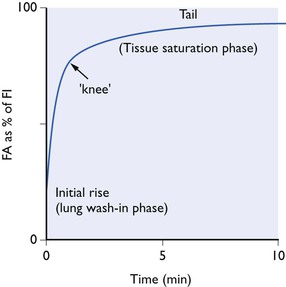
Figure 3.2 Typical alveolar tension curve for an inert gas inhaled at a fixed concentration from a non-rebreathing system.
Blood solubility and alveolar tension
The shape of curve obtained with any given anaesthetic depends on a number of factors. These include such things as minute volume of respiration, the functional residual capacity of the lungs, the cardiac output and the blood flow to the main anaesthetic absorbing bulk of the body – muscles and fat. However, one physical property of the anaesthetic itself is considerably more important than all of these factors – the solubility of the anaesthetic in the blood. This is the factor that determines the height of the ‘knee’ in the alveolar uptake curve. With anaesthetics of low blood solubility the knee is high; with high solubility the knee is low. This may be illustrated by consideration of the hypothetical extremes of solubility.
A totally insoluble gas would not diffuse into the pulmonary blood and would not be carried in it away from the lungs. If such a gas were inhaled at a constant inspired tension in a non-rebreathing system, its alveolar tension would increase exponentially as lung washout proceeded until, after a very short time, alveolar tension equalled inspired tension (Fig. 3.3). The curve obtained would be all initial rise and there would be no tail. Such a gas could not ever be an anaesthetic, since none would ever reach the brain.
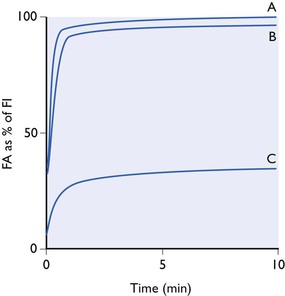
Figure 3.3 Alveolar tension curves for a totally insoluble gas (A), of low solubility (B), (nitrous oxide) and a gas of extremely high solubility (C), all breathed at a constant inspired concentration from a non-rebreathing system.
A gas of extremely low blood solubility (see Fig. 3.3, curve B) would give an almost identical curve. The loss into the pulmonary bloodstream of only a minute amount of the gas contained in the lungs at any moment would bring the tension of the gas in the blood into equilibrium with that in the alveolar air. The capacity of the blood for such a gas would be extremely small. Likewise, the capacity of the entire body tissue (with the possible exception of fat) would be small, since as already pointed out, the tissue–blood partition coefficients of most anaesthetics are close to unity. If such an agent, even when given at the highest permissible concentration of 80% with 20% of oxygen, only produced a faint depression of the central nervous system, it could nevertheless be looked upon as a very active agent because it would be deriving its effect through the presence in the brain of only a minute trace.
At the other hypothetical extreme would be a gas of very nearly infinite solubility in blood. All but a very small fraction of the gas in the lungs at any one moment would dissolve in the pulmonary blood as soon as the blood arrived at the alveoli. The capacity of the blood and body tissues for such a gas would be vast. The alveoli tension curve (see Fig. 3.3, C) would be very flat, with virtually no rapid initial rise and a very slowly rising tail. Given enough time for full equilibrium, it might be possible to achieve very deep anaesthesia by using a minute inspired tension but, of course, in one sense, the gas would be a very weak anaesthetic, since its concentration in the brain would be enormous.
Ranging between these hypothetical extremes of solubility are the gaseous and volatile anaesthetics. Their solubilities in blood and tissues for humans and some animals (figures taken from various sources but mainly from data sheets) are shown in Table 3.1. The effect of the different solubilities on the alveolar tension when the agents are administered at a constant inspired tension are shown in Figure 3.4.
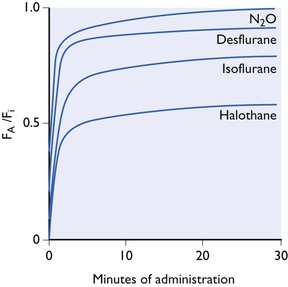
Figure 3.4 Increase in alveolar tension (FA) towards inspired tension (FI) during administration at a fixed concentration in a non-rebreathing system. Effect of blood solubility. The curves are not drawn accurately and only represent approximate, relative curves.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree