The Biomechanics of the Equine Limb and Its Effect on Lameness

Chapter 26 The Biomechanics of the Equine Limb and Its Effect on Lameness



Alan Wilson, Renate Weller


Biological structures (and sometimes those engineered by man) break, as a result of either a one-off (single event) load that exceeds their mechanical capacity or, more commonly, chronic fatigue overload, in which repeat microfailures over time lead to failure of the whole structure. Biological tissue has the unique ability to adapt to mechanical demands and to repair itself given an appropriate mechanical stimulus and sufficient time. Complete failure of a structure happens only if the damage over time exceeds adaptation and repair.


Like man-made structures (e.g., elevators, bridges), biological designs have an inherent safety factor, defined as the ratio of the maximum stress a structure could withstand until breakage and the stress it is most likely to undergo during its lifetime. It is rather comforting that most engineered devices have a safety factor of up to 10 (so next time you read that an elevator has a maximum capacity of 18 people, know that it would actually hold 180!). Unfortunately, the safety factors1 of equine bones and tendons are approximately 1.5 to 2.


Box 26-1 provides short definitions of biomechanical terms used in this chapter.



BOX 26-1 Definition of Common Terms in Biomechanics



Duty factor: Ratio of stance time and stride time. Expressed as either a fraction (between 0 and 1) or a percentage (between 0% and 100%).

Ground reaction force: Reaction force exerted from the ground onto the limb of a horse as a reaction of the force exerted by the horse onto the ground. Often split into three components: vertical (weight support), craniocaudal (acceleration and deceleration), and mediolateral (turning and balancing).

Kinetics: Study of the forces acting on bodies.

Kinematics: Study of the movement of bodies.

Safety factor: Ratio of a structure’s strength to the maximum stress that the structure is likely to experience over its lifetime.

Stance phase (contact phase): Time the limb is in contact with the ground, from initial contact (foot on) to liftoff (toe off).

Stiffness: Force required to achieve a certain change in length. Slope of the force-length curve; the stiffer the structure, the higher the stiffness and the steeper the force-length curve.

Strain: Length change of a structure in relation to its starting length (e.g., through compressive or tensile load), often expressed as a percentage of the original length of the structure.

Stress: Force per unit area; also called pressure.

Stride time (duration): Time taken for a full stride cycle—for example, between foot contact of a limb to the following foot contact of the same limb. In general, the stride time decreases with increasing speed.

Swing phase (protraction): Time the limb is not in contact with the ground.

Stride frequency: Number of strides taken per second, measured in strides per second or Hz.


When Do Musculoskeletal Structures Fail?


The parameters that influence failure of a musculoskeletal element are the force (magnitude, frequency and number of cycles, speed and duration of loading) the structure experiences and its ability to withstand it. The force on an individual part is related to the force that the whole limb experiences. Force is determined by body mass, speed of locomotion, and the leverage that force has on the specific part. A structure’s ability to withstand force is determined by its structural properties, which in turn depend on its material properties and its dimensions. These reflect the magnitude and direction of the forces acting on it. Forces causing deformation include tension, compression, bending, and shear. Most structures are subjected to and are optimized for one predominant force, but they also have to be able to withstand other forces in normal use and even more so in exceptional circumstances. Tendons experience predominantly tensile forces, whereas joints are subjected to mainly compressive and some shear forces. Bones experience bending, with compressive forces on the concave side and tensile forces on the convex side. Bones have to withstand not only compressive forces from the horse’s weight, but also the forces exerted by muscles and tendons that attach to them.


Failure in a live horse is much more complex than simple mechanics, because adaptation, repair, and compensatory mechanisms must be considered. Lameness may be not only a response to pain but also a compensatory mechanism, because it often results in an unloading of the affected limb or structure.


Elements of the musculoskeletal system have to fulfill four main requirements: force transmission without excessive deformation and fracture; use of the least amount of material to keep the metabolic costs for maintenance, transport, and regeneration down; and enough reserve of strength to cope with overload in the case of an accident.2 Thus there is a trade-off between safety factors and energy costs. In horses the balance is shifted in favor of keeping the energy costs low while accepting a relatively high risk of musculoskeletal injury. Tendons (such as the equine digital flexor tendons or the human Achilles tendon) need to stretch to store energy in locomotion; to perform this role they need to reach high strains, which places them at a high risk for mechanical overload and damage.


In the following sections we describe the functional anatomy of the horse’s limb and the material properties of its components. We discuss the influence of locomotion and the effects of conformation and farriery intervention on the loads acting on the musculoskeletal elements, such as bones, tendons, and joints. We also consider how the loads acting on the musculoskeletal system are changed with certain musculoskeletal disorders.



Functional Anatomy of the Horse Limb


Horses have the ability to run fast over short distances (racing speeds reach 21 m/sec [75 km/hr]) and also to cover long distances at slower speeds with a low energy cost of locomotion. This was of evolutionary advantage because it enabled them not only to outrun predators but also to migrate to forage on the rather sparsely vegetated prairie land they originally inhabited. To achieve two diverse locomotive requirements, the horse developed anatomical features that promoted energy efficiency (after all, it would not do the horse any good if it had to spend more energy to get to the food than could be gained by eating the food, or to get eaten in the process).


Although most veterinarians are familiar with some energy-saving mechanisms, such as the unguligrade stance of the horse, the patellar locking mechanism, and the stay (reciprocal) apparatus, from standard textbooks, there are many more features that play a major role in ensuring energy-efficient locomotion. This section concentrates on the musculoskeletal adaptations of the equine limb; however, a more comprehensive overview of general anatomical features is given elsewhere.3



Horse Limbs Function Like Pogo Sticks


If you tried to build a horse limb with children’s blocks, the limb would collapse, because it would be impossible to build the fetlock joint in a hyperextended position. However, in a live limb the digital flexor tendons and ligaments on the flexor side of the limb prevent failure. Tendons have elastic properties and act like rubber bands or springs, providing resistance against which the limb presses when it comes under load, thus resisting further hyperextension and preventing collapse (Figure 26-1). The tendons are stretched at the same time, thus storing elastic strain energy, which can be returned in elastic recoil. During each step energy is stored, and it is returned when the limb leaves the ground. Energy is carried forward from one step to the next, thus reducing work the muscles have to do and saving metabolic energy. Indeed, the muscles associated with the main contributors of this system—the suspensory ligament (SL), deep digital flexor tendon (DDFT), and superficial digital flexor tendon (SDFT)—either are not present at all (the SL and the accessory ligament of the DDFT [ALDDFT]) or are very short in relation to the tendons (e.g., the average length of the deep digital flexor muscle-tendon unit in a Thoroughbred is 77 ± 5 cm, more than 60% of which is tendon. The flexor muscles, being highly pennate and having short muscle fibers (1 cm in length), have limited capacity to change the length of the muscle-tendon unit when contracting. Approximately 7% of the energy stored in the tendons is released as heat, and during gallop the tendons of a galloping horse reach about 45°C.4 We have reasoned that increase in temperature may account for core lesions in equine SDFTs but found that although 45°C resulted in death of some cells, tendon cells may be resistant.5 Core lesions may result from hyperthermic damage of matrix components.5


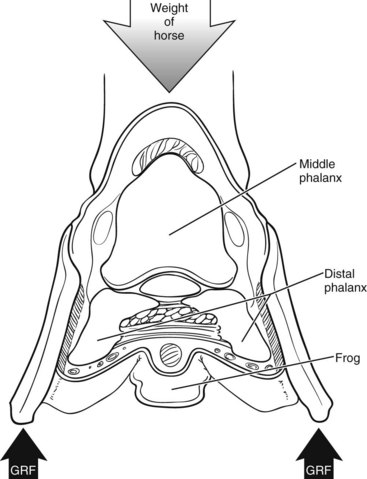
image

Fig. 26-1 Anatomical drawing of an equine forelimb (left) and the equine forelimb modeled as a spring-system (right); superficial digital flexor tendon (SDFT); deep digital flexor tendon (DDFT); accessory ligament (AL) of the DDFT; and AL of the SDFT. Limbs function like pogo sticks: the hyperextended fetlock joint is kept from collapsing by the springlike digital flexor tendons on the palmar aspect of the limb. When the limb comes under load during the stance phase of the stride, it compresses by further extending the fetlock joint while stretching the digital flexor tendons. This enables the digital flexor tendons to store elastic energy, which is released for propelling the limb into the swing phase. MCP, Metacarpophalangeal; PIP, proximal interphalangeal; DIP, distal interphalangeal.


Like any springlike structure, the limb itself has a certain stiffness, which is a measure of how much it shortens for a given load. A whole equine limb changes length mainly as a result of fetlock extension and length changes in the digital flexor tendons.6 People can adjust their leg stiffness by muscle contraction to suit the softness or hardness of the ground on which they are walking or running.7 Horses cannot adjust their leg stiffness because of the limited ability of the flexor muscles/tendons to change length, and this may be the reason why some horses cope better than others on different goings (footings). The flexor muscles do, however, damp vibrations, which otherwise would be likely to cause injury to musculoskeletal tissues.8



Bones


To enable a pogo-stick design, the bones in the equine limb are reduced compared with other animals: the radius and ulna are fused, and the horse bears weight only on the third metacarpal bone (McIII) or third metatarsal bone and the digit. Fewer bones allow lengthening of the limb and tendons and reduction of the mass of the distal aspect of the limb. This increases the energy storage capabilities of the digital flexor tendons and also results in a lighter limb that can be swung more rapidly and with less energetic cost, which is of benefit in locomotion. Fewer bones is thus an adaptation for maximum strength with minimum weight, because the bending strength is much higher for one large bone than for the same amount (and hence weight) of material arranged as several smaller bones.2 However, a reduction in bone mass for energy efficiency results in an increase in fracture risk, and this is reflected in the fact that the distal limb bones are at higher risk for fracture than the proximal limb bones.9



Synovial Joints


Joints fulfill two main mechanical functions: they allow the movement of limb segments in relation to each other, and they act as shock absorbers. Limb movement is limited to the sagittal plane by anatomical adaptations of the phalanges and the fusion of bones, and only small, out-of-plane movements, such as adduction and abduction or rotation, are possible. Movement is further limited by the anatomical features of some of the articular surfaces, such as the interlocking configuration of trochlear and sagittal ridges and matching grooves, and is enforced by collateral ligaments. Without the need for muscular control, these features restrict joint movement to the sagittal plane, thus further decreasing metabolic costs.


Although all joints provide movement and shock absorption to a certain degree, some joints allow only a small range of movement and have the primary function of shock absorption, whereas other joints have a large range of movement and a primary function of movement. These joints can be functionally classified as low-motion or high-motion joints, respectively. The fetlock joint, a good example of a high-motion joint, goes through 90 degrees of movement during the stance phase of gallop, whereas the proximal interphalangeal joint has a range of motion of only 5 to 10 degrees. In complex joints such as the carpus and tarsus, there is a division in function: both the antebrachiocarpal and tarsocrural joints are high-motion joints, but in the more distal joints of the carpus and tarsus there is less movement; the least movement is in the carpometacarpal and tarsometatarsal joints. There is also a difference in occurrence and clinical severity of skeletal disorders between high- and low-motion joints. Osteochrondrosis is much more common in high-motion joints, and osteoarthritis (OA) is usually of greater clinical significance than in low-motion joints.



The Foot as Interface to the Ground


The foot provides the interface between the horse and the ground. It is a complex modification of integument surrounding, supporting, and protecting structures in the distal limb of the horse. The hoof capsule encases within a confined space three bones, a series of ligaments and tendons, two synovial structures, a digital cushion, cartilages of the foot, blood vessels, and nerves. Although the horny hoof capsule provides protection of the internal structures, it does not allow for expansion through swelling; therefore any swelling that does occur as a result of injury leads to an increase in pressure and thus stimulation of pain receptors. Mechanically the foot has three main functions: shock absorption when the foot comes into contact with the ground, support and grip when the limb is bearing weight, and propulsion when the limb leaves the ground. It must also resist excessive abrasion and protect sensitive structures lying internally, while, in wild horses, allowing sufficient natural wear of the wall to maintain hoof shape.10


The foot has a series of “built-in” protective mechanisms that absorb part of the concussive forces and damp vibrations during impact (Figure 26-2):


1 The shape of the solar surface with the frog in the middle and the frog sulci (grooves) on either side allows the heel to move sideways and distally on ground contact while the toe retracts.

2 The suspension of the distal phalanx within the horn capsule allows forces to be transferred from the distal phalanx across the laminar junction to the hoof and to the ground via the distal border of the hoof wall.

3 The digital cushion located under the frog and sole between the cartilages of the foot is a wedge of elastic subcutaneous tissue, consisting of collagen, elastic fibers, islands of cartilage, fat, and modified skin glands; this cushion aids in shock absorption by deforming and permitting the frog to move. The equine digital cushion, however, is small in comparison to that in other species—for example, the elephant limb, which relies heavily on its large digital cushion for shock absorption.

4 The hoof has the ability to slide along the ground surface.

5 The distal interphalangeal (DIP) joint can move by rotation and translation.

image

Fig. 26-2 Schematic drawing illustrating two of the shock-absorbing features of the equine foot. First, the shape of the solar surface with the frog in the middle and the frog grooves on either side allows the heels to move sideways and distally on ground contact, while the toe retracts. Second, the suspension of the distal phalanx within the horn capsule allows forces to be transferred from the distal phalanx across the laminar junction to the hoof and to the ground via the distal border of the hoof wall. GRF, Ground reaction force.



Ability of Structures to Cope with Mechanical Demands



Structural and Material Properties


When a force is applied to a structure, the structure usually responds by deforming. The greater the force applied to a structure, the greater the deformation. The ability of a structure to resist deformation is expressed as stiffness and represents the slope of a structure’s force-length relationship. The force-deformation relationship of biological structures behaves in a roughly linear elastic manner until the applied load causes nonreversible deformation and ends in failure. The force-deformation relationship describes the structural properties and depends on the material properties of a tendon and on its dimensions. Larger structures are able to cope with larger forces: imagine two ropes made of the same material, but double the cross-sectional area (approximately 1.41 times the diameter): the thicker rope will be able to withstand double the force of the thinner one.


It is often of interest to know about the properties of the material per se, independent of size. This is achieved by dividing the force acting on a structure by its cross-sectional area. When normalized for cross-sectional area, a force is called stress (σ; common units would be mega Newtons per square meter [MN/m2] or Newtons per square millimeter [N/mm2]). The resulting deformation of an applied stress is expressed as strain (ε), the ratio of the change in size to the original size. Being a ratio, strain does not have a dimension; however, it is often expressed as a percentage—for example, ε = 0.1 = 10%. If we are interested in the property of a material rather than structure, we can express this relationship as a stress-strain curve. The slope of this curve is the ratio between the tensile stress and strain and is called the elastic modulus or Young’s modulus (E). The elastic modulus defines whether a material is “rigid” or “compliant.” Rigid materials have a very high elastic modulus and deform very little under load, whereas compliant materials have a low elastic modulus and require less load to deform. Bone, for example, is relatively rigid, whereas articular cartilage is more compliant and thus is able to act as an excellent shock absorber by undergoing considerable deformation when under load. Figure 68-1 shows the stress-strain curves for the digital flexor tendons of a Thoroughbred racehorse.


The ability of structures to deform when loaded and return to their original length when the load is removed allows them to store energy. The amount of energy per unit volume is the area under the linear portion of the stress-strain curve. The capacity of a material to absorb and release energy is often referred to as elastic resilience. The energy a material can absorb before failure defines whether it is “brittle” or “tough”: tough materials are able to absorb considerable elastic energy before failing, whereas brittle materials absorb very little. The digital flexor tendons of a horse are able to store and return a considerable amount of energy during locomotion. Load-deformation curves of tendons are different between loading and unloading, forming a “hysteresis” loop. The area of the loop presents the loss of energy, largely in the form of heat, that occurs during stretch and release (see Figure 68-2). It has been shown that the heat produced by repetition of this mechanism leads to an increase in core temperature, which may contribute to the pathogenesis of tendon injury through thermal damage.4 A detailed description of the pathobiology of tendon injuries is given in Chapter 68.


From an injury perspective, stress is probably the most informative mechanical measure in addition to strain. Equine digital flexor tendons, for example, have different elastic moduli and experience different strain rates in vivo, but they also have different cross-sectional areas. Both the SL and the SDFT experience high strains (up to 16%) during locomotion, but the stress in the SDFT is much higher than in the SL because its cross-sectional area is only about a third of that of the SL.11 This corresponds to the fact that the SDFT is the most commonly injured tendon or ligament (see Chapter 68).



Changes in Structural Properties

You may also need

Tags:
Jun 4, 2016 | Posted by in EQUINE MEDICINE | Comments Off on The Biomechanics of the Equine Limb and Its Effect on Lameness
Premium Wordpress Themes by UFO Themes