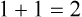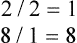Calculations and Conversions

CHAPTER 24


image


Calculations and Conversions



Learning Objectives


Mastery of the content in this chapter will enable the reader to:


• Calculate monthly finance charges.


• Calculate accounts receivable percentages.


• Calculate inventory turns per year.


• Develop an effective product markup.


• Develop an effective service markup.


• Calculate cost/benefit ratio.


• Calculate a break-even analysis.


• Calculate payroll.


• Calculate drug doses.


• Calculate intravenous fluid doses.


Every team member should be familiar with the common calculations that are used in veterinary practice. Receptionists and office managers are generally responsible for determining finance and statement charges for client account receivables. They may also be responsible for product markup when products are special ordered for a client. Office managers may be responsible for payroll and for determining the cost/benefit ratio of special promotions or the purchase of equipment. Each team member must be familiar with drug calculations and equations because every team member must double-check medications before they leave the premises; this can prevent a fatal mistake.


Most of the following equations have been covered in previous chapters. The purpose of this chapter is to allow the reader to become comfortable with equations used in everyday practice. The reader should practice the examples given because practice results in improved skills. Math can be a difficult task, but with a little practice anyone can become proficient at conversions and calculations (Box 24-1).



Box 24-1   Common Conversions




kg, Kilogram; g, gram; mg, milligram; mcg, microgram; lb, pound; L, liter; dL, deciliter; mL, milliliter; mcL, microliter; cc, cubic centimeter; gtt, drop; T, tablespoon; t, teaspoon; gal, gallon; qt, quart; pt, pint; oz, ounce; fl oz, fluid ounce; c, cup; m, meter; cm, centimeter; mm, millimeter.


Many of the conversions should be memorized by team members; this will allow tasks to be completed more easily. A copy of the conversion table can be hung in a central location in the veterinary practice so that all team members can benefit. Conversion tables also provide a way to double-check work.



MONTHLY FINANCE CHARGES


Monthly statement fees must cover the cost of the statement being produced. This includes team member time, paper, ink, stamps, and envelopes. It may also be encouraged to add a finance fee; credit cards charge finance fees, why shouldn’t a veterinary practice? State regulations must be verified as to what percentage of a bill is allowed as a finance charge.


Items to consider when determining the cost of a statement fee:



Example A: What minimum dollar amount should be added in order to recover costs associate with monthly statements?



Labor:$12×6hours=$72×20%=$14.40


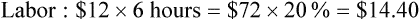
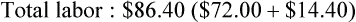
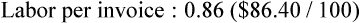
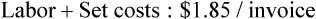
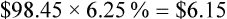
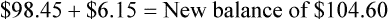
image

Total labor:$86.40($72.00+$14.40)


image

Labor per invoice:0.86($86.40/100)


image

Labor+Set costs:$1.85/invoice


image

A statement fee of at least $1.85 must be applied to each invoice to recover costs. If the practice chooses to use a finance fee instead, the following would apply:



$98.45×6.25%=$6.15


image

$98.45+$6.15=New balance of$104.60


image

If a practice wishes to use both a monthly statement fee and finance charge:


$98.45+$6.15+$1.85=$106.45


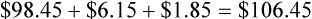
image

Example B: What is the client’s new balance after monthly statement fees have been printed?



Labor:$9×3hours=$27×20%=$5.40


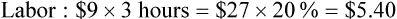
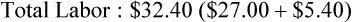
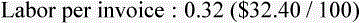
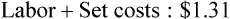
image

Total Labor:$32.40($27.00+$5.40)


image

Labor per invoice:0.32($32.40/100)


image

Labor+Set costs:$1.31


image

The practice chooses to have a set monthly fee of $5 per invoice and no monthly finance charge.



$354.08+$5=New balance$359.08


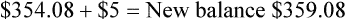
image


Practice Set: Monthly Statement Fees


Determine the minimum monthly statement fee and the new balance based on the following scenarios. Answers appear on the Evolve site accompanying this text. image




ACCOUNTS RECEIVABLE PERCENTAGES


What percentage of the gross revenue is tied up in accounts receivable?


Less than 0.5% of gross revenue should be tied up in accounts receivable. A practice that produces $895,000 per year should have a total of only $4475 in accounts receivable each month! If the amount were 3%, it would total $26,850 per month. It should be the goal of every clinic to have the lowest accounts receivable possible!


$895,000×0.5%=$4475


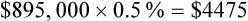
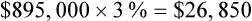
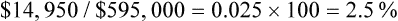
image

$895,000×3%=$26,850


image

Example A:


Gross revenue (GR) for a veterinary practice is $595,000; accounts receivable (AR) total is $14,950. What is the percentage tied up in AR?


$14,950/$595,000=0.025×100=2.5%


image

The AR total is divided by the total GR to obtain a numerical amount (don’t forget, to obtain a percentage the numerical answer must be multiplied by 100).


Example B:


GR for a practice is $1,902,798.98. AR is 3%. What is the total dollar amount tied up in AR?


$1,902,798.98×3%=$57,083.97total AR


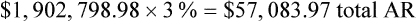
image

Example C:


The predicted GR for a practice is $800,000 and the practice’s goal is to keep accounts receivable less than 1%. What amount can the AR total to meet this goal?


$800,000×1%=$8000


image



INVENTORY TURNS PER YEAR


Turns per year is defined as the number of times an inventoried product turns over in a practice. This helps determine correct reorder quantities and points. Each practice should set a goal of eight to 12 turns per year. To determine the inventory turns per year, the beginning inventory is added to the ending inventory and the result is divided by two. This results in the average inventory per year. The total amount of product purchased during that period divided by the average yields the number of turns per year for that product. Taking the equation one step further, dividing the number of days in the year (365) by the number of turns per year produces the average shelf life of the item.


Example A:



4+1=5


image

5/2=2.535/2.5=14


image

Keflex turned over 14 times during 2007.


Example B:



2+2=4


image

4/2=236/2=18


image

The product turned 18 times. This is an excellent value!


Example C:



1+1=2


image

2/2=18/1=8


image

The product turned eight times during 2007.



DEVELOPING AN EFFECTIVE PRODUCT MARKUP


The markup of a product is defined as the cost (of the product) multiplied by a percentage calculated to recover hidden costs associated with inventory management. Many practices will mark products up 100% to 200%. A product markup must be at least 40% to break even. Shopped items, such as vaccines and routine surgeries, should be kept competitive with the local or regional veterinary practices. Nonshopped items must be increased to accommodate the lower priced shopped items. Special services and supplies must be marked up appropriately to cover the extra charges that generally accommodate the special service.


Example A:


A tablet of acepromazine costs the practice $0.10 per tablet.



Example B:


A bottle of Rimadyl costs the practice $86.




Dispensing Fees


Practices may also add a product dispensing fee as well as a minimum prescription charge. The average dispensing fee ranges from $8 to $14 to cover the cost of the label, the pill vial, and the time used to count the medication. If a bottle of shampoo or a full bottle of medication is dispensed, the average dispensing fee ranges from $3 to $5. Many practices initiate a minimum prescription fee of $14 to $18 to help recover hidden pharmacy costs.


Hidden pharmacy costs include costs associated with expired medications, ordering and shipping costs, and insurance and taxes on products and supplies. These costs can increase rapidly and must be covered.


Example A:



$1.06×100%=$1.06


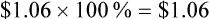
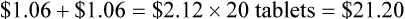
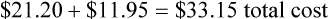
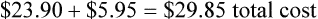
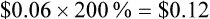
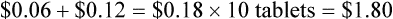
image

$1.06+$1.06=$2.12×20tablets=$21.20


image

$21.20+$11.95=$33.15total cost


image

(The prescription met the minimum prescription charge; therefore the additional charge was not needed.)


Example B:



$11.95×100%=$11.95


image

$11.95+$11.95=$23.90


image

$23.90+$5.95=$29.85total cost


image

(The prescription met the minimum prescription charge; therefore the additional charge was not needed.)


Example C:



$0.06×200%=$0.12


image

$0.06+$0.12=$0.18×10tablets=$1.80


image

Related posts:

  1. Veterinary Ethics and Legal Issues
  2. Controlled Substances
  3. Outside Diagnostic Laboratory Services
  4. Preparing and Maintaining a Budget

Stay updated, free articles. Join our Telegram channel
Tags:
Oct 1, 2016 | Posted by in EXOTIC, WILD, ZOO | Comments Off on Calculations and Conversions

Full access? Get Clinical Tree
Get Clinical Tree app for offline access