(1)
Mathematics in Naples, Naples, Italy
Deceased
After having shown that all heavy bodies by their nature are equally rapid, it remains to find out how and why heavy bodies which move in fluid environments have unequal velocities. We will attempt at supplying as best as we can these physical and mechanical explanations which hitherto were missing.
Proposition CCXIV
Homogeneous fluids flow from vertical pipes of the same diameter at velocities proportional to the square root of the lengths of the pipe as long, however, as the pipes remain full of fluid.
At first it must be observed and investigated why and at what velocities fluids move in pipes or siphons. Two pipes are taken the cavities and orifices of which are equal. Both are continuously full and a fluid, for example water, flows out while the pipes are vertical and their orifices are horizontal. From both orifices, in equal times, volumes of water flow out not in the ratio of the heights, as experience shows, but in the ratio of their square roots. If the height of the longer pipe is four times that of the other, the velocity at which water flows out of the orifice of the longer is not four times but only twice the velocity at which water flows out of the lower orifice of the shorter pipe. From this it is deduced that the fluids in vertical pipes of unequal lengths have the same nature as pendulums the properties of which we presented elsewhere.
Proposition CCXV
The flow of water inside a pipe is quicker about the axis than close to the inner surface of the pipe.
Before proceeding further it must be noticed that water flows more quickly downwards in the middle of the cavity of the pipe, about its axis, than towards the surface of the cavity. As said above, the cohesion of water adhering to the rugged inner surface of the pipe slows down the descent and flow of the water more than in the central part of the cavity where the particles of water are impeded by each other with an insensible pertinacity only. This appears from a double experiment. Firstly, at the upper orifice of a narrow pipe the surface of the water is excavated like a cup whereas at the exit of the fluid the surface of the water bulges downwards like a cone or a turgid eminence. This could not occur if the central parts of water did not flow more easily than the side parts close and adhering to the inner surface, which, as we said, are retained and suspended in some way by the stable asperity of the pipe so that their flowing is impeded.
Proposition CCXVI
Explanation why water is not dispersed in the subjacent air after its exit from a pipe but is gradually narrowed until it breaks.
After a fluid has begun to flow out freely in the air from the lower orifice of a pipe, it must be conceived that any surface or small layer of the fluid is led to the open air at a degree of velocity which depends on the length of the pipe or pendulum. The same applies to all the following layers of water when they are led to the boundary with air. All the layer of water after having gone out thus ought to part from the surface of the other water layer which follows it and comes out of the pipe in the open air just after it. The reason is that the first layer while flowing and travelling in the air a distance equal to its own thickness in a given time necessarily acquires a greater degree of velocity corresponding to the movement and the said time. But in the same position the second layer of water at the exit of the pipe lacks this degree of velocity which the first layer acquired. Consequently, in the second period of time equal to the first, the first layer of water will travel a distance thrice as long as that which it travelled at first and which the second layer must travel, because in the second period of time it moves at a degree of velocity twice stronger than that at which the following layer falls. But, from the beginning the two layers were contiguous. Consequently, in the second period of time they should separate from each other. Since this does not occur there must unquestionably be a cause which maintains them tied together. This cause of course is the cohesion and the small viscosity mentioned above by which the parts of a fluid adhere and are bound to each other. The fact that these parts of water flowing out of the pipe move at unequal velocities but cannot separate from each other results in the thinning which is observed in the water after its exit from the pipe. Therefore, this water is more and more tapered. But now it must be explained why the flowing water in its progression, after being reduced to such slim line, breaks into several parts and droplets. Here it must be admitted that the force of the cohesion, since it is small, cannot resist the impetuosity of the continuously increasing velocity in the fall of the water. This impetuosity thus can disrupt the union in which the water moved at first, at the place where the cohesion was weakened by some external cause or the velocity of the flowing is modified and slowed down by an external impediment.
The movement of the water flowing in the air outside the pipe adds nothing to our matter. Therefore, leaving the digression, the other phenomena of water flowing in pipes must be described.
Proposition CCXVII
Equal masses of water flow out at an equal velocity from pipes of unequal diameters but of equal height the lower orifices of which are equal and horizontal.
Firstly, it must be noticed that in these pipes the lower orifices perpendicular to the direction of the flow of the liquid getting out of the pipe come alone under scrutiny. It is ignored whether the inner cavities are larger than the orifices themselves (indeed here we do not deal with pipes dilated below like a cone). One must take into account that portion of water which flows downwards and not that which is immobile. For example, if we consider a vertical glass pipe and an equally deep cistern in the bottom of which a hole is drilled equal to the lower orifice of the pipe, the water flows from the hole in the cistern at about the same velocity and in the same volume as the water which leaves the glass pipe equally full. In the water of the cistern one must imagine a vertical pipe between the hole below and the surface of the water. Only the water contained in the imaginary pipe flows. What remains on the sides is supported by the impenetrable and firm bottom of the cistern which prevents vertical flowing of the water. Therefore, the water moves vertically as if it were contained in a glass pipe. It is true, however, that the inner hard surface of the glass pipe impedes the outflow of water by its asperity more than the water walls of the imaginary pipe in the cistern do. This is the reason why in very narrow pipes and very thin canals water not only flows out slowly but sometimes its movement and fall are completely prevented, as we mentioned above.
Proposition CCXVIII
In similar pipes unequally inclined on the horizon the velocities of the flowing water are in the ratio of the square roots not of their lengths but of their vertical heights.
If two similar pipes are unequally inclined on the horizon the flow of water is proportional to the square roots not of their length but of their vertical height. Galileo and Torricelli demonstrated that, if a mobile is displaced over an inclined and a vertical plane, both of the same height, if either movement begins from rest, the mobile will acquire the same degree of velocity at the end of either descent. From this it appears that in two pipes unequally inclined on the horizon, the velocities at which the fluid gets out of the lower orifices must correspond, not to the lengths of the pipes but to their heights.
Proposition CCXIX
The velocities at which water gets out of the lower orifices of pipes are the same as those at which the same water moves inside the cavities of the canals.
Equal volumes of water always get out of the lower orifice of the same pipe in equal times. On the other hand, water flows from its higher level at one and the same well-determined velocity (as long as the pipes are supposed always to be full). Therefore, in equal times the same volume of water is poured in above as that which gets out from the pipe below. Thus, in the process of moving inside the pipe, the water flows at the same velocity at which it gets out below. This velocity is determined by the height of the fall, or the length of the pendulum, or of the pipe. Consequently, the velocity of water inside the canal of the pipe has always the same degree, equal to that which corresponds to the length of the pipe. Then, so as to make the next propositions more easy to demonstrate, it must firstly be supposed as evident that two equal volumes of water got out in equal times must necessarily have got out at equal velocities from the same pipe orifice perpendicular to the direction of the flowing water. Conversely, if the velocities are equal, the volumes of water which flowed out in equal times will also be equal. Thus, a double volume of water also gets out of an equal orifice at a double velocity in the same time. The same is true for equal multiples in the same ratio. If the velocity is a fraction of another velocity, the ratio of the volumes of water getting out of equal orifices in the same time will also be equal to the ratio of the velocities.
Similarly, if two equal volumes of water get out from the same orifice at the same velocity, the durations of their outflow will be equal and conversely. The same is true if the durations and volumes of water flowing out at the same velocity are equal multiples in the same ratio.
Proposition CCXX
If two equal volumes of water flow at unequal velocities out of two equal orifices of pipes in equal times, the volumes of water are proportional to the velocities.
Let the pipes AB and CD have equal lower orifices B and D (Table 11.1, Fig. 1). Their planes are not oblique to the direction of the movement of the water flowing out of them but are perpendicular to these directions. (This is supposed so in all subsequent propositions). A volume of water R flows out of AB at a velocity M in a time T. In the same time a smaller volume of water S falls from CD at a velocity N. It must be shown that the ratio of the volumes of water R/S is equal to the ratio of the velocities M/N. Let another velocity H be taken and another volume of water O such that H is a multiple of N and O is the same multiple of S. It appears that, in the same time T, a volume of water O flows out of an orifice equal to B at a velocity H while a volume of water S flows out of D at a velocity N. If the velocity H is equal to the velocity M, two equal volumes of water O and R will flow in the same time out of B at the two velocities H and M. If actually the volume O flows in the same time at a velocity H greater than M, the water O is also more than R. If the velocity H is smaller than M, the volume of water O is also smaller than R since they flow from the orifice B in the same time. There are four quantities M, N, R, S and two other quantities H and O are taken which are in the same commonly measurable ratio to the denominators N and S. They are together, either equal to or greater or smaller than the numerators of the series. Consequently, M/N = R/S.
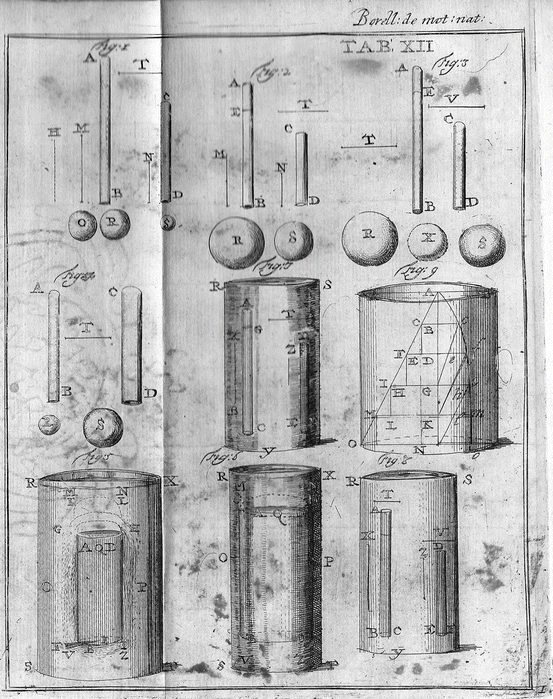
Table 11.1

Proposition CCXXI
From the same pipes, in equal times, volumes of water flow out proportional to the square roots of the lengths of the pipes.
Let two unequal pipes, a longer AB and a shorter CD stand vertically (Table 11.1, Fig. 2). Their lower orifices B and D are equal. The pipes always remain full. In the same time T a volume of water R gets out of the orifice B and a volume of water S from the orifice D. A height EB is taken at the level of the proportional average between the heights AB and CD. It appears that AB/EB is equal to the ratio of the square root of AB to that of CD. I claim that the ratio of the volumes of water R/S flowing out in the same time T is equal to the ratio of the heights AB/BE. Let M be the velocity corresponding to the length of the pipe AB and N the velocity corresponding to the pipe CD. Since the ratio of the velocity M of the water flowing through the orifice B to the velocity N of the water flowing through the orifice D equal to B, the pipes remaining full, is equal to the ratio of the square roots of the heights of the pipes AB/CD, the ratio of the velocities M/N = AB/BE. But the ratio of the volumes of water flowing through the equal orifices B and D in the same time is equal to the ratio of their velocities. Thus, the ratio of the volumes of water R/S flowing out in the same time T is equal to the ratio of the heights AB/EB. Q.E.D.
Proposition CCXXII
The ratio of unequal volumes of water flowed out of the same pipe is equal to the ratio of the durations of their outflows.
Let a volume of water R get out from the orifice B of a pipe AB in a time T and a volume of water S in a time V (Table 10.1, Fig. 9). I claim that the ratio of the volumes R/S is equal to the ratio of the times T/V. The height of the pipe AB remaining the same, water must always flow from its orifice B equally large at one and the same velocity M. Taking as previously H and O which are the same multiples of the time V and of the volume of water S, it is concluded that the ratio of the times T/V is equal to the ratio of the volumes of water R/S.
Proposition CCXXIII
If two pipes of unequal heights have equal orifices and equal volumes of water get out of them, the ratio of the durations of the outflows is equal to the inverse ratio of the square roots of the heights.
Let the height of the pipe AB be more than that of CD (Table 11.1, Fig. 3). Their orifices B and D are equal. From B a volume of water R gets out in a time T. From D a volume of water S equal to R flows out in a time V. As previously, BE is the proportional average between AB and CD. I claim that the ratio of the times V/T is equal to EB/CD. Let the volume of water X be that which flows out of the orifice D in the time T. Consequently, the ratio of the volumes of water R/X is equal to the ratio of the heights EB/CD. From the same orifice D of the pipe CD two volumes of water X and S get out in the times T and V. Thus, the ratio of the volumes of water S/R is equal to the ratio of the times V/T. By hypothesis the volumes of water R and S are equal. Consequently, they form the same ratio with the same volume X. But EB/CD = R/X and V/T = S/X. Thus, the ratio of the heights EB/CD is equal to the ratio of the times V/T.
Proposition CCXXIV
Two volumes of water getting out of the unequal orifices of pipes of equal heights flow at equal velocities. Their ratio will be equal to the ratio of the orifices.
Let two pipes AB and CD have the same height but the lower orifice B be smaller than the other orifice D (Table 11.1, Fig. 4). In the same time T a volume of water R flows from B and a volume of water S from D. I claim that they flow at the same velocity through the pipes and the ratio of the volumes of water R/S is equal to the ratio of the sizes of the orifices B/D. The flows of water have equal velocities as a result of the equal heights of the pipes AB and CD. Actually, volumes of equal velocities flow in the same time through the unequal orifices B and D. Consequently, the ratio of the volumes R/S is equal to the ratio of the sizes of the orifices B/D.
After these premises, to enable us to determine the velocities at which bodies of the same specific weight rise and fall in a fluid, firstly we must examine more accurately the structure and the mechanical action of the siphon and balance constituted by the solid and the adjacent fluid in which this solid rises and falls.
Proposition CCXXV
A solid cylinder constitutes with an equal volume of ambient water a circular balance and a tubular siphon the orifice of which is equal to the base of the solid cylinder. The fulcrum of the balance is the point on the circle separating the fluid from the solid which undergo opposite movements.
Proceeding to the structure of a balance or a siphon in floating bodies, let a large vessel RSTX full of water be imagined into which a solid and consistent body ABCD, cylindrical for facility’s sake, is immersed (Table 11.1, Fig. 5). Its specific weight is smaller than that of water. This solid cannot be raised unless the incumbent water AKLD is expelled from its position and returns below to refill the space BC left by the solid. Consequently, the surrounding water must flow downwards everywhere over all the sides AB and DC. Therefore, this forms not one siphon alone but countless ones or rather a round siphon the outer part of water of which constitutes a hollow tube AFCH. The inner solid part ABCD is the other part of the siphon which rises upwards while the water flows downwards through the tubular siphon. Obviously all the adjacent water does not descend in a large vessel while the wood rises, but only a small part close to and surrounding the cylinder AC. This can be recognized in muddy water. The remaining immobile water plays the role of a vessel. But it is not evident that the water tube AFCH constituting the siphon is exactly equal to the wooden cylinder AC. Therefore, we will try and show it by reasoning. The solid AC rises by as much as the volume of water which is expelled from above and this volume is equal to that which flows downwards to refill the space left. While moving from AD up to KL the wood expels from above the water cylinder AKLD. This water by pushing the water in front of it moves to refill the space left by the base BC, as occurs in a solid wheel or in a circular siphon. But the water AKLD leaves its upper position at a certain and well-determined velocity, that at which the cylinder AC rises. Thus, when displaced downwards over the sides from AG towards FB, the water does not seem to have to move at a smaller or greater velocity than that which it had developed and had in its descent from the upper position KD, since it is neither impeded nor impelled by the balanced adjacent water of the vessel nor by the subjacent one which flows in the siphon spontaneously by virtue of the excess of its moment. Consequently, if in the same time the fluid and the solid travel equal distances in the siphon, the former rising and the latter descending, they are of course equal. This indeed could not happen unless the canals of the siphons were equal and equally large. From this it is deduced that the orifices of the siphons, the solid one and the fluid one, are equal, i.e. the size of the flowing water is equal to the size of the solid.
To find the fulcrum of this siphon one must conceive a physical radius of the moving water and of the solid cylinder FE. The fulcrum of the balance falls at its midpoint B separating water and wood. Equal masses of wood BEQA and water FBAG rest on equal bases BE and FB. These masses carry out equal but opposite movements. The solid rises by as much as the adjacent water descends. If the solid has the same specific weight as water, it is as if the portion of water FBAG were of the same substance as the wood BEQA or, conversely, as if the wood were water. Then it appears that the centre of gravity of the aggregate made of the wood and the adjacent water equal to the wood is exactly on the vertical through the centre of the balance or fulcrum B. Then there is no reason for the equilibrium to be disturbed. Therefore, neither the wood rises nor the water descends. On the contrary, the fluid remains undisturbed in the same position. If the wood has a lesser specific weight than the adjacent water, the common centre of gravity of the solid and fluid is no longer on the vertical through the fulcrum B of the subjacent balance, as it was previously. It falls beyond this vertical towards F. Then, according to the nature of the pendulum, it tips the balance FE or rather the water descends in the siphon and the wood rises.
What was said of the physical radius or sector FE must be said of all the other parts of the surrounding water as well as of the wooden cylinder. They thus constitute countless balances or rather a superficial balance the fulcrum of which is the circumference of the circle described by the radius EB. This seems to be always true in large vessels as long as the rising solids have an oblong and evenly wide figure, i.e. if they are prisms or cylinders. For conical or curved figures a discrepancy is found as will appear below.
Proposition CCXXVI
On the other hand, in very narrow vessels the size of the water siphon surrounding the solid and flowing downwards must be smaller than the base of the solid but they must react in opposite order to their velocities.
To understand this, let us suppose a pipe or a narrow cylindrical glass vessel RSTX full of water in which a wooden cylinder ABCD is immersed (Table 11.1, Fig. 6). The square of the radius QA of the base of the cylinder is greater than the rectangle KDL. It indeed appears that the circle of the base AD is larger than the circular area KLDA. Therefore, the size of the siphon of flowing water is smaller than the size of the rising solid cylinder. The solid cylinder rises in the water by as much as the volume of water AGHD is expelled from its upper position. Consequently, since the top of the cylinder AD moves vertically to the position GH, a water cylinder AGHD must be expelled from its position. The base of this water cylinder is equal to AD. Actually, to move downwards this upper water has to flow through the lateral straits and, in the same time during which the water AGHD is expelled from its upper position, it will occupy the adjacent hollow cylindrical space AKOPLD. Since this water tube is equal to the water cylinder AGHD, their bases must necessarily be inversely proportional to their heights. Thus the ratio of the base of the water tube KLDA to the base AD of the water cylinder AH is equal to the ratio of the height AG of the latter to the height KO of the former, i.e. equal to the ratio of the rising or velocity of the wooden cylinder AC to the flow of the descending water in the tubular siphon. Thus, the narrowness of the vessel can be such that the velocity of the flow of water downwards becomes hundreds and thousands of times greater than that at which the solid cylinder rises. Consequently, if the velocity of the flow of water downwards is determined by the height of the siphon AB, i.e. if this velocity has one well-determined degree, which is generally agreed on, the wooden cylinder must necessarily rise in the water that much more slowly. This is nicely confirmed by experience. Moreover, it seems that the velocity of the rising wood can also be slowed down by another cause, namely by the asperity of the inner surface of the vessel. Inasmuch as the particles of water are not completely deprived of cohesion, as mentioned above, they cannot flow through the narrow passages and asperity easily. These thus can slow down the rising of the wood much more.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


