(1)
Mathematics in Naples, Naples, Italy
Deceased
Hitherto we considered the gravity, not of all fluid bodies, but only of water, quicksilver and others similar the ponderousness of which nobody questions. Obviously they strive downwards and descend. A problem arises concerning other bodies which seem to move upwards such as wood and others which rise in water. To attribute gravity to them appears to be against common sense. Nevertheless, with the best known philosophers, we shall attempt to show that all elementary fluid bodies are provided with gravity and that there is absolutely no positive lightness in nature. It must also be shown that all elementary bodies have the force to unite to form our system, i.e. they have the motive faculty of descending towards the centre of the terrestrial globe. This force is called gravity. Firstly, we shall examine the arguments of Aristotle expressed against Plato and Democritus who asserted the above mentioned opinions. Then we shall recall for examination the arguments of Aristotle himself by which he attempted to establish positive lightness. Thirdly, I will bring forwards demonstrations which show that there is no positive lightness. Finally, I will consider all which was indistinctly presented by the best peripatetics against the Platonic opinion and which led to my own idea.
Aristotle criticized the position of Democritus and Plato but in his own way. He argued not against their opinion, but against their wording of it, namely that the gravity of earth is greater than that of air results from an abundance of triangles which is greater in the earth than in the air. He considered these triangles as if they were flat surfaces absolutely indivisible. This appears to be false since in the Platonic opinion the triangular atoms are bodies rather than indivisible surfaces.
Moreover, against Democritus he said that a huge mass of air such as would be an aerial sphere having a diameter of ten cubits has a greater abundance of full and substance than a small ball of water having a diameter of one finger breadth. Therefore, the aerial ball should be heavier and descend whereas the water being lighter should rise. I claim that this argument was not presented by Democritus who never dreamed such nonsense. He indeed never considered full substance alone but a huge mass of vacuum increased by full substance in the huge ball of air, and always in a greater ratio than that of the full substance of air to the full substance of water. Aristotle passed with little sincerity over the exception in silence since, in the presence of air rarer than water, the ratio of the empty part to the full part of air is greater than the ratio of the empty part to the full part of water. Conversely, the ratio of the empty mass of air to the empty mass of water is greater than the ratio of the full mass of air to the full mass of water. Therefore, a mass of air, however large, has more cause for lightness than water if one admits that this cause is vacuum. On the other hand, in the same air the cause of gravity will be weaker. The cause of gravity results from the full substance and is measured by it. Therefore, in the large sphere of air together with addition of full part ten times greater than in the small ball of water, an opposite cause is added, that of lightness which is a vacuum more than thousand times bigger than the vacuum contained in water. Consequently, the proportion of vacuum exceeds so much the other proportion of fullness in these two elements that the huge ball of air will never be heavier as a result of an increase of its fullness and its material part since it also contains in itself the opposite cause which makes it much lighter and is much more increased. This cause is emptiness and vacuum. The long series of arguments presented so many times by Aristotle against the Ancients are of the same flour.
Moreover, it is not true that the Ancients attributed movement or a virtue of action to empty space. They conceded this virtue to a material and full principle. This appears obviously from Aristotle himself. He indeed mentions that the Ancients supposed that all the elementary bodies are heavy and ponderous, more or less, depending on whether the full and material principle was sparse or abundant in them. He also said that, according to the Ancients, the rising of some bodies, namely the fire, did not result from some positive principle, i.e. lightness, but that this ascent was a consequence of an extrusion carried out by heavier ambient fluid bodies. If indeed this was the opinion of the Ancients, how can they be attributed the enormous nonsense that vacuum moves, impels, has a position and a region towards which it strives? How could those who publicly said that all natural movements of the elementary bodies tend downwards, that all result from one single positive principle, namely fullness and material substance, claim this? And, since air is pushed and extruded upwards, that consequently the vacua contained in air move upwards and rise? If vacuum is nothing else than space, this will be immobile and, therefore, will not carry vacuum upwards with itself. It will rather acquire new spaces by relinquishing the previous ones which are absolutely immobile. If the word vacuum means pure absence of fullness, or nothing, it is certain that nothing can neither move nor impel nor migrate from one place to another.
After considering the arguments of Aristotle against the Ancients who denied absolutely any positive lightness, it remains to consider the reasons of Aristotle for supporting and asserting lightness. The main reason is that there are two opposite positions in nature: upwards and downwards, i.e. the circumference and the centre of the world or of the earth. Obviously the earth appears to be lower and is situated below all the other worldly bodies. By descending it sinks below air and water down to the centre if not impeded. Hence Aristotle deduced that earth is absolutely and simply heavy, not relatively. On the other hand, we see that air penetrates the density of water itself and rises above it, and fire drills through the density either of water or of air and is brought through to the supreme and extreme surface of air, as to its supreme natural position, where it finally remains immobile and does not move further. Since fire towers above everything, he says, fire is thus simply and absolutely light. Earth is situated below everything and is thus absolutely heavy.
In order to understand and judge exactly the force and energy of the reasoning of Aristotle, we must remember the state of the controversy, namely the thesis of Plato and Democritus which Aristotle takes the opportunity to refute, before considering the argument used by Aristotle. Firstly, it must be admitted that fire can be led upwards in two ways and tower above all elements. Either fire moves spontaneously upwards from an intrinsic and natural principle, namely lightness, or rather fire is expelled there and extruded by the greater gravity of the other fluid bodies such as air and water. The latter was the opinion of Plato and Democritus which Aristotle attempted to refute. But the argument of Aristotle attacks and condemns a proposition completely different which nobody questions. He presented nothing else than a phenomenon which is obvious and which his adversaries admitted, namely that we all see that fire rises above air. Aristotle tried rather to demonstrate that fire rises, not because it is extruded by a heavier fluid environment and is impelled upwards, but because it is moved spontaneously by its own lightness which does not exist. The argument of Aristotle thus can be called a petition rather than a demonstration.
To add vigour and force to this reasoning of Aristotle, some peripatetics say that it is absolute nonsense that natural bodies are moved to their proper places, not by an intrinsic principle ingrained in them by nature, but by the violence of an external body during their extrusion. From this it is deduced that nature is deficient in such necessary and useful operations since it needs stimuli, violent impulse and constraint. Since these include resistance and violence, the operation does not seem to be natural and, therefore, neither perpetual, nor useful to the order and conservation of the universe.
To this specious reasoning it can be answered that the rule according to which, where actions and operations do not occur spontaneously but violently, one must then conclude that the said operations are not carried out by nature and a natural principle, is untrue.
In one word, the operation which is carried out with some violence is also natural.
Proposition XXXVIII
Although some violence intervenes in the ascent of wood in water, all this operation is nevertheless natural.
This can be confirmed by the following reasoning. If it were true that any operation in which some violence is used should be considered as being unnatural, none of the alterations of solid bodies and also of the generations of plants and animals would be nor could be called a natural operation since always an action, a distortion of the qualities and a corruption of the preceding substance are required. Unquestionably, however, these said passions and corruptions are violent operations carried out, not willingly, but with some inconvenience and suffering. In all these operations, nature itself thus exerts violence. Therefore, it must be admitted that the proper behaviour of nature consists of exerting violence so that without it nature does not know how to do anything and is unable to pursue its goals.
But, some people insist, it is accidental that nature destroys a previous shape because it cannot generate the next shape if the initial one persists. Firstly, they say, nature by itself acts for the good and for its end and generation. Therefore, a preceding corruption is like a prerequisite without which the next shape can neither be introduced nor generated. They thus claim that at least nature exerts violent actions by accident. But that all that which is done by nature is called natural action. Consequently, this accidental violence by which a previous shape is destroyed is also a natural action and operation. According to the common saying, who wants the end also necessarily wants the means which lead to this end. Thus, the natural instinct by which generation of a shape is sought for and achieved, necessarily involves violence, at least as a necessary prerequisite. This enables one to deduce that it is neither absurd nor indecent that nature exerts some violence in order to achieve a greater good by means of this violence. If this is true for alterations and corruptions, according to me, it is even more verified in other more pleasant actions of nature, when natural bodies are led to their positions for the good and convenience of these bodies violently agitated. Similarly, somebody carried home from the market place in a cart or a litter would be ill advised to complain of coercion and violence, since this violence will result for him in usefulness and pleasure. In about the same way light bodies are led to their due position by heavy bodies descending naturally.
Proposition XXXIX
The violence with which wood and air rise in water is called natural because it is necessary.
These sayings are in agreement with the common Peripatetic opinion. But anybody who carefully considers this matter clearly perceives that the word violence metaphorically discloses an origin from the unpleasant feeling of pain and bitterness which animals suffer when they are altered and corrupted. Consequently, where feeling is absent, there must be no pain nor violence. Therefore, natural operations should be distinguished from unnatural or violent ones according to another safer and more precise rule such as follows: all the operations which are absolutely and completely necessary, which Nature cannot avoid and is necessarily forced to exert, must be legitimately called natural and considered as such.
The natural operation by which heavier bodies descend lower and become closer to the centre of the earth than lighter bodies, necessarily entails an ordered arrangement of the bodies such that the heavier ones occupy the lower position and the less heavy ones the upper position. Moreover, this universal correct arrangement requires that both bodies, by striving downwards, move in their common centre of gravity. Similarly, in a balance loaded with unequal weights, rising of the smaller weight results from the descent of the heavier body loading the other scale of the balance. This is incorrectly called injury and violence since this operation and arrangement are necessary and normal.
The same or something similar must be said of the extrusion of any less heavy body achieved by the pressure of a heavier ambient fluid. In such instance, as will be shown in due place, there is a perpetual imaginary balance the centre of gravity of which is progressively lowered. The descent necessarily results in a movement of rising of the less heavy body. This persists until equilibrium is achieved. The necessary and natural effect is the extrusion or rising of the wood whenever it is surrounded by a heavier fluid. This rising cannot and must not be called or designated as violent. Q.E.D. This can be confirmed by the most beautiful reasoning of Galileo.
Proposition XL
The rising movement of heavy bodies is not less natural than their descent.
Imagine that the globe of our earth is drilled through by a well passing across its centre and led to the antipodes. An iron ball is dropped in it. Unquestionably, its natural gravity will acquire a greater and greater impetus until it reaches the centre of the earth. All this motion is considered as being natural because it results from its intrinsic principle of gravity. But after attaining the centre of the earth the ball will of course not stop there. The impetus acquired in its preceding descent will carry it beyond the centre and the ball will run towards the antipodes. But in this course, the ball while receding from the centre of the earth unquestionably will rise. This ascent is called a violent movement. It is against its nature but results, however, from the natural operation of descent.
This can be confirmed by other examples which can be easily experimented.
Let a vessel RSXV be full of water (Table 3.1, Fig. 6). A wooden cylinder EF immersed in water will not sink completely below the upper surface RS of the water. A part of it will remain surging above the surface since the wood has a specific weight smaller than water (as Archimedes said). If I raise the wooden cylinder out of the water up to the position AB and then drop it, the cylinder will not stop and remain immobile in the position EF. The impetus acquired in falling in the air will send the cylinder more deeply below the surface of the water in a violent movement, down to the position CD. From there it will rise again, pass beyond its position of equilibrium EF and resile completely outside the water almost to the position AB, and this again and again until, after weaker and weaker ups and downs, it finally remains immobile in its natural position EF.
In the same way a pendulum AB can move about its firm centre A (Table 3.1, Fig. 7). The leaden ball B is moved from its natural vertical position and brought to the elevated position C. The ball, being heavy, will describe the arc CB while descending. All this movement is natural since it results from the intrinsic impetus of gravity. But the ball will not remain in the lowest position B after being brought back there. It will describe further a distance almost equal to its previous distance from the vertical, up to the position D, rising from the lowest position B over all the arc BD. This which is generated by an intrinsic and natural principle cannot be natural. The rising of the ball beyond the centre of the earth, the descent of the cylinder EF below the surface of the water after its fall and the rising of the leaden ball over the arc BD result from, and are created by, the natural virtue of gravity of the descending body as long as it is descending. No intervening extrinsic cause which induces violence and impels the heavy body upwards can be imagined other than the impetus acquired and conceived in the fall occurring naturally and provoked by the intrinsic principle of gravity. Unquestionably, the impetus resulting from a natural principle is also natural and intrinsic. Consequently, the operation of rising is natural in so far as it results from, and is created by, an intrinsic principle. In this case, violence could be considered only if it was generated by a foreign and outside principle.
A distinguished Peripatetic objects to this reasoning and says that the subsequent ascent beyond the centre of the earth, or beyond the vertical over the arc BD does neither result from nor is generated by the gravity of the body but by the impetus conceived during the downwards movement. He says that this impetus is a thing by far different from gravity. Indeed this impetus struggles against gravity.
It is obviously conceded to this opponent that the rising of the ball after passing beyond the centre or beyond the vertical is carried out and produced by the virtue of the impressed impetus which is the immediate cause and the principle of this rising. This operation is called lightness. But, besides the immediate cause of this rising, i.e. besides the impetus, the cause producing this impetus must also be noticed. This is the natural and intrinsic gravity of the body. Thus this is at least the mediate cause of the final rising. Here I notice that the opponent neither denies nor asserts that gravity was the cause and the producing principle of the impetus. He only says that gravity is very different from impetus, that their natures are opposite and annihilate each other since the subsequent upwards movement of the ball or of the pendulum ceases only because the gravity of the ball annihilates the force of the upwards impetus in an opposite effort. But what does finally the opponent want to deduce from this? Is it that, since the nature of gravity is different from the impetus, we shall say that the impetus of the ball descending down to the centre or beyond the perpendicular was not generated by the force and the action of gravity? But by what virtue was it generated as if it was by an immediate principle? Of course if we do not want to deny common sense, it must be recognized that this impetus was generated, not by another cause or an external principle, but only by the gravity itself of the descending ball. The certitude of common sense must not be relinquished because of the problem brought forwards by the opponent, as Aristotle clearly recommended. If thus the gravity of the ball is at least the principle and the mediate cause of the consequent rising, the act and operation of rising which is judged as violent and beyond the nature of a stone, is carried out and generated by the internal and natural principle of its gravity. Therefore, the act of rising or the violent movement is carried out by an internal and natural principle.
Here, by the way, the self-confidence of these philosophers can surprise. On the one hand they deny that the impetus is generated by gravity and teach that they are very different and annihilate each other. On the other hand, together with Aristotle, they publicly say that in mechanics the impetus is a flowing gravity and thus is of the same nature since a stone provided with an impetus compresses and squeezes the opposite bodies in the same way as an incumbent weight does.
But, the opponent insists, how can gravity carry out an impetus by which a ball rises, whereas we see that this rising movement is progressively weakened and finally extinguished because of the resistance and opposite action which the weight of the ball achieves? I answer that the action of its weight, i.e. its compression, produces two opposite effects. Firstly, during the descent it creates, enhances and increases its impetus. Afterwards, during the ascent, it works against it, weakens and annihilates it. Although this seems surprising, they nevertheless concede that this is necessary, willy-nilly, as appears to common sense. The hand when pushing a falling stone increases and multiplies its impetus. But if the stone rose the same hand would weaken and annihilate its impetus in an opposite movement. Similarly, the same heat of the sun generates and increases the plants and then desiccates and kills them. This shows the shortcoming of the reasoning presented above.
Proposition XLI
Rising and raising of light bodies can be carried out by the same principle of gravity.
But now I return to the proposition and I will try to explain it by another argument. The most common saying of all the philosophers is that nature always produces its operations by the shortest way with he utmost conciseness and it abhors prolixity and multiplication of causes when able to produce its effects through a shorter and easier way. Consequently, if natural bodies can possibly be carried to their proper positions by means of one single motive virtue of gravity, nature would act vainly and stupidly if it attempted to attain this end by using two principles, namely gravity and an opposite virtue called lightness. Natural bodies can be brought to their natural positions by gravity alone without lightness. This appears from what was said above. Indeed the smaller gravity which is assigned to a bladder full of air, the greater gravity of water and the greatest of all attributed to quicksilver is a more than sufficient cause able to produce the effect thus mentioned which results from mechanical principles and arguments. Therefore, it must be admitted with great likeliness that nature attains its purpose of placing the earthly bodies in their due places, upwards and downwards, by the principle of gravity alone without any lightness.
Hitherto, the likely reasons against positive lightness have been presented. It remains to demonstrate the same point directly by more convincing and more efficient reasons.
Proposition XLII
Firstly, we shall show that any body moved spontaneously by an intrinsic and natural principle is displaced more easily and more quickly in a rarer and thinner fluid than in a thick and more resistant fluid environment.
Of two vessels let one GHIK be filled with water, the other KILM with quicksilver (Table 3.1, Fig. 8). The same wooden ball A is immersed in both. Two volumes B and C of these fluids, each equal to A, are thought of as lying above A. The mass C of mercury obviously is heavier, more resistant and more compact than the mass B of water. Moreover, the wooden ball A cannot rise without expelling the water B from its position to take its place and move to occupy the space B equal to itself. This always happens. In its rising the ball A is forced in a continuous upwards effort to impel an incumbent volume of water equal to itself and to penetrate its pertinacity. The magnitude of the natural impetus of the lightness of this wood is supposed to be D. The moving body A provided with the impetus D impels the fluid body B which, being immobile, opposes its natural inertia to the impulse of the impelling light body A. According to what was demonstrated in the book On the Force of Percussion, the motive force of the light body A thus is transmitted and distributed in all the moved body, i.e. in the fluid B. Consequently, the impetus D is considerably weakened and slowed down. The velocity E at which the light wood A and the fluid B move is decreased. For the same reason the velocity F at which the same wood A and the mass of mercury C equal to A move is slowed down. It must be shown that the velocity E at which the wood rises through the water is greater than the velocity F at which the wood rises in the mercury. The ratio of the velocities E/F is about the inverse ratio of the material substance AC to the weight of AB. The two bodies A and B are impelled by the same motive virtue by which the single wooden mass A was supposed to move initially and to which the natural degree of impetus D corresponded. Consequently, the ratio of the sum of the material masses of the two bodies A and B to the material mass A is the inverse ratio of their velocities, thus D/E. By the same reasoning, the ratio of the material masses A/AC is equal to the ratio of the velocities F/D. Thus after changing the terms of the equation, the ratio of the material masses AB/AC is equal to the ratio of the velocities F/E. The material substance AB is smaller than that contained in AC. Therefore, the impetus F is smaller than E. Consequently, the wood A displaced in the mercury C must rise more slowly, at a smaller velocity than the velocity E at which the wood rises in the water B.
It is of course obvious that any body carried in a spontaneous movement by an intrinsic principle is displaced and moves much more easily through a rare and yielding fluid environment than in a more tenacious and thicker fluid environment. A ball of gold falls more rapidly the same distance through air than through water and more quickly through water than through mercury. Animals also which are moved by an intrinsic force can walk more uneasily when submerged by sand, less uneasily in mud, more easily in water and much more easily in air. The opposite can never occur, i.e. that the same animal exerting the same motive force moves more uneasily and more slowly through air than through water and more uneasily through water than through mud or through quicksilver.
Proposition XLIII
The bodies called light are not moved upwards by an intrinsic lightness.
After this we shall consider wax or a bladder full of air rising through different environments. If it is true that a bladder of air rises in water or in quicksilver in a spontaneous movement, i.e. by an intrinsic motive virtue called lightness, in rising it necessarily must penetrate the intermediate fluid bodies and overcome their tenacity and density. It must expel the fluid from its position to make its own way and passage so as to be able to rise and pass. Since quicksilver is much more concentrated, denser and heavier than water, any light body full of air or participating in the nature of air such as wood or wax (which according to the opinion of the opponents are moved by an intrinsic virtue of lightness), they necessarily must meet greater resistance when passing through quicksilver. Their degree of impetus is necessarily blunted and slowed down much more by its tenacity, density and weight than occurs when rising through water. This, being rarer and more yielding, weakens and slows down less their motive force. Therefore, the ascending movement of wood or wax through quicksilver will be slowed down much more than that through water. But this is untrue and against evidence. The movement of wood or wax through quicksilver is quicker than through water indeed. Consequently, it is not true that they are moved upwards by an intrinsic and natural principle and, therefore, the cause of the rising is not positive lightness. Such lightness has no use in nature and, therefore, does not exist.
Proposition XLIV
For a reason of mechanics, a mobile is expressed upwards more quickly by a heavier fluid than by a less heavy one.
Problems of this kind can be avoided and escaped from if we stick to the certitude and necessity resulting from the principles of mechanics. If gravity is supposed to be present in all sublunary bodies, the heaviest fluid, quicksilver, necessarily must impel wood upwards during its squeezing out with a greater impetus than another less heavy fluid such as water. On a balance, a weight of one ounce is also impelled upwards at a greater velocity by the greater opposite compression of a weight of ten pounds than by the smaller compression of a weight of one pound. The demonstration of this matter will be presented in due place. Meanwhile, all the effects which are observed in these rising bodies are the same and comply to the same mechanical laws as if all were heavy bodies provided with unequal gravities. Moreover, the phenomena of movement do not seem to occur in them for the reason which would be required if, besides gravity, another opposite principle of lightness was also found. Consequently, it must be admitted that nature acts with gravity alone and does not require any lightness.
There are people who, in order to hold to the unlikeliness of their position, raise problems and objections against the evidence of these reasons. They say that wood would have had to rise more slowly in quicksilver than in water because of the greater resistance of quicksilver. But, because of its aversion and hostility towards mercury, wood accelerates its course to escape mercury sooner and attain water and air which is a friendly element; therefore, hatred having ceased, wood is not forced to leave this element at the quickest. But see how these philosophers are easy going. When occasion requires, they do not hesitate to answer otherwise. Indeed, if I ask why gravity which is certainly present in these earthly bodies moves a stone more quickly where it comes closer to the earth, they answer: because in the vicinity of the earth the motive force of the falling stone is as if it were strengthened. The lightness of a bladder of air should also increase near the surface of water since it comes then closer to air and, therefore, its motive virtue should also be strengthened. But, omitting this, different bodies can be taken which have a nature and a character different from and contrary to water, more similar to mercury, such perhaps as a glass bottle or a bladder which is filled with sublimate or precipitate mercury. The vessel could also be made of metal or of another body more similar to mercury so as to result in a composite the nature of which is very different from water and very similar to mercury. The hostility and aversion between the vessel and the thicker mercury fluid would thus be completely suppressed. Nevertheless, this vessel will be observed to rise more quickly through quicksilver, and slowly through water. Consequently, the cause of the inequality of the movements is not this dreamed of hostility but the mechanical and natural necessity by which the greatest weight of quicksilver expresses and impels upwards in a more impetuous movement the glass vessel or the bladder contained in it than water is able to impel it because of its smaller weight.
The same point can be confirmed by other examples. Oil condensed and frozen by the cold has a character and a nature which is rather comparable to heavier mercury or to oil of tartar and would thus, on the other hand, have a nature contrary to and different from water. So this oil, because of its affinity, should rise slowly through quicksilver or through oil of tartar. But it should move very quickly in water in so far as water is contrary to oil. Lime contained in a bladder is very similar to aqua fortis because of the heat and bitterness of both, and is, on the other hand, very contrary to fresh water. Nevertheless it rises very quickly in aqua fortis acid and slowly in fresh water. Small vessels of wax or bitumen could also be taken. They could be filled with powder, spirit, oil or wine or countless other substances which always rise very quickly in heavier fluids such as aqua regia. Although they are similar by their extreme heat and their salty bitterness, they rise slowly in fluids of a contrary nature as long as they are less heavy. Therefore, it is not true that a bladder of air shuns mercury because of their hostility and opposition and moves slowly through water which is similar to itself. This occurs rather for a mechanical reason resulting from a greater or smaller gravity. This is deduced from the theory of Archimedes: a heavier fluid must impel upwards and extrude less heavy bodies. This is the cause why bodies must move upwards without positive lightness.
Against the evidence of this reasoning some people object firstly that, as heavier bodies immersed in less heavy bodies are carried upwards with a force equal to the difference between the gravity of the mobile and that of its environment, it is evident that this will occur proportionally in lighter bodies contained in less light bodies. These will rise in the order of their lightness, they will not strive upwards according to the measure of their difference with the less light effort upwards, as results from the same reasoning. After this supposition he gives a seemingly sure and obvious answer to the argument brought forwards above and says that the expired air, very light as related to water, according to the measure of all its lightness, strives upwards in water. Therefore, it succeeds in overcoming swiftly the resistance of water. The very small excess in lightness over the ambient air strives upwards exactly according to the measure of this excess. Therefore, it is not surprising that it rises through the air even if it is said to be moved by an intrinsic positive lightness.
Thus, so as we deduce from the theory of Archimedes, the reason of the descent of the heavy bodies and the ascent of the light bodies from the hypothesis that all sublunary bodies are heavy, they are convinced to be able to demonstrate the same phenomena by supposing that not only the rising bodies but also the fluid environment in which they rise are light. Therefore, whenever dealing with falling heavy bodies, the gravity of the mobile body and that of the fluid environment in which it descends must be compared. On the contrary, when dealing with ascending bodies, their lightness must be compared with each other and with the lightness of the fluid environment in which they rise.
To expose the fallacy of this reasoning I will firstly demonstrate some mechanical lemmata from which, using the hypotheses mentioned above, I will then demonstrate that it is absolutely impossible that the impetus of the velocity at which these bodies which are called light rise can be produced by and result from some intrinsic principle by which they are impelled upwards and moved away from the centre of the earth.
And firstly, I observe with Aristotle in his mechanics that:
Proposition XLV
The opposite extremities of a balance or a wheel must rotate in opposite directions about the centre.
Let a balance with equal arms or a wheel AIBH rotatable about its centre C be considered (Table 3.1, Fig. 9). Obviously, if we wish to rotate the balance or the wheel so that its extremity A moves downwards, describing the arc AI, its opposite extremity B must necessarily move upwards in an opposite movement, describing the arc BH equal to its counterpart AI. Whenever these contrary movements cannot be carried out together, the balance or the wheel must necessarily remain immobile in the same position.
Proposition XLVI
If forces pulling in opposite directions are applied at the same extremity of a balance and impede each other, the greater force will prevail and tip the balance with a force equal to the difference of the forces.
A weight DE is put at the extremity A of a balance (Table 3.1, Fig. 9). This of course exerts a force and tries to pull the extremity A of the balance in the direction AD towards the centre of the earth. But, since the radius AC is fixed at the centre of the balance, this results in a rotation of the balance. The extremity A is carried not over the straight line AD but over the arc AI, travelling a whole quadrant. Since the balance AB is supposed to be continuous and rigid all the time during which the extremity A describes the arc AI, the opposite extremity B will describe the opposite arc BH. We can prevent the movement of the balance and the descent of the weight DE by applying at the extremity A an opposite force G which would pull upwards the extremity A over the same vertical line towards the uppermost point G. If the force and motive faculty G were equal to the force of the weight DE, there would be no reason for one of the virtues to prevail over the other. Then the extremity A of the balance will neither descend towards I nor rise towards H but will remain immobile in the same position. If the weight DE prevailed over the motive force G and its excess over G was the weight E, then unquestionably the weight DE would prevail and overcome the motive force G. The impetus and force which would tip the balance downwards towards I would be measured by the force of the weight E which is the excess of the compressing weight DE over the raising force G.
Proposition XLVII
If two forces pull the opposite extremities of a balance or a wheel, both striving downwards, they impede each other. The greater force will prevail but by a force equal to their difference.
Descent of the weight DE can be prevented and impeded in another way without applying a contrary animated force C at the extremity A (Table 3.1, Fig. 10). This occurs if another weight F is set at the opposite extremity B. This other weight, while impelling downwards in the same direction as the weight DE, prevents also the descent of the extremity A of the balance, as was said. If the weight F is equal to the weight DE, there is equilibrium since both weights attempt at moving downwards and at displacing the two extremities of the balance towards the lowest point of the quadrant I. They act with equal force and impetus. Unquestionably, one force and effort prevents the displacement and descent of the other. This mutual impediment results in immobility of all the balance in a horizontal position. But if the weight F is equal to a part D of all the weight DE, the bigger weight prevails and the extremity A of the balance tips towards I. The opposite extremity B rises towards H with a force equal to the excess of weight E. Consequently, in a balance or a wheel, equal impulses striving in the same direction, namely downwards, and similar to each other, impede and neutralize each other, thus resulting in immobility. If the forces of these similar downwards movements are unequal, the bigger weight prevails and tips the balance not with all its force but only with the difference or excess of the bigger weight over the smaller.
Proposition XLVIII
The data are the same. If the two forces pull upwards the result is the same.
This is true also if, at the opposite extremities of the same balance AB, two unequal forces, DE bigger and F smaller, are applied both of which pull the extremities of the balance upwards (Table 4.1, Fig. 1). It will be shown in the same way that the balance tips upwards from A towards H and that the smaller force F is overcome by the excess of the virtue DE over F. The extremity B descends towards I.
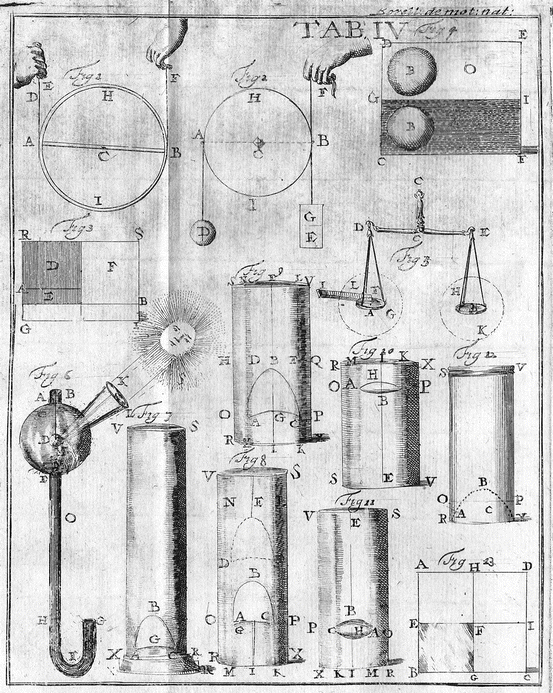
Table 4.1

Proposition XLIX
If two forces pull the opposite extremities of a balance, one upwards, the other downwards, they enhance each other and the force tipping the balance is equal to the sum of the two forces.
Thirdly, the extremity A of the wheel or balance AB is pulled downwards by the weight D but its opposite extremity B is pulled upwards by the ascending force F which is smaller than the weight D (Table 4.1, Fig. 2). I claim that the balance is not immobile but tips: its extremity A descends towards I and its opposite extremity B is raised towards H. The effort or force by which the balance tips is equal, not to the difference or excess of the weight D over the force F, but to the sum of the two forces D + F. At the extremity B a weight E is applied, equal to the force F impelling upwards. Another weight G equal to the opposite weight D is also suspended there. It is obvious that, after the opposed forces F and E are removed or neutralized, the equal weights D and G hanging from the extremities of the equal arms of the balance achieve equilibrium. The balance thus is immobile. Moreover, the weight E is equal to the contrary force F pulling upwards and both are applied at the extremity B of the scales AB which is balanced by the equal weights D and G. Consequently, the sum of the two weights G + E impels the scales in a contrary effort from B towards I. They are precisely equal to the effort of the weight D and the pulling force F both of which can lower the extremity A of the balance towards I while raising the extremity B towards H. Thus the sum of the two forces D + F, after the weights G and E are removed, determine the force or the effort by which the balance must rotate from A towards I.
Here it must be noticed that the two forces D and F which are contrary to each other (since the former compresses downwards and the latter pulls upwards) do not oppose each other. One does not impede the movement of the other but promotes, enhances and increases the effort, force and impetus of the other. This occurs because both are not applied at the same extremity A of the scales but at the opposite extremities A and B which, according to the property and nature of a balance or a wheel, must carry out contrary movements, namely A over the arc AI and B over the arc BH. Consequently, the downwards impulse of the weight D and the pull exerted upwards by the force F concur. They enhance and increase each other so that both carry out the rotation of the balance which is impelled in the same direction by these contrary forces. Thus, one must stop wondering why, in a balance, two contrary forces do not neutralize each other but rather enhance each other so that they both result into one composite force which tips the balance.
Proposition L
If four forces pull the opposite extremities of a balance, two upwards and two downwards, the effort or the force tipping the balance is measured by the sum of the difference of the two forces upwards and the difference of the two forces downwards.
Finally, the balance is impelled and pulled by four forces (Table 3.1, Fig. 11). The two weights D and G strive downwards. The two forces M and F pull the extremities of the balance upwards. The energy of force M is greater than F. The weight D is smaller than G. Obviously, the extremity A is raised towards H by the excess of the force M over the motive faculty F. On the other hand, the opposite extremity B of the balance is lowered towards I by the excess of the weight G over the force of gravity D. The two impulses are different and contrary, one upwards, the other downwards, and they are applied at the opposite extremities of the same balance. Consequently, they enhance and promote each other. Therefore, the effort, force and impetus by which all the balance tips is equal to the sum of the said differences.
Proposition LI
The motive force by which a solid with a specific weight higher than that of the fluid descends is equal to the difference of the weight of the solid and the weight of a volume of fluid equal to that of the solid.
The vessel RGS is full of water (Table 4.1, Fig. 3). A heavy, hard and consistent body DE is immersed in it. This body is heavier than the adjacent water F. According to what was said in Prop. 9 and to Archimedes, the two weights DE and F are set in an imaginary and perpetual balance AB in which the excess of the weight of the solid DE over the gravity of the same volume of water F as the volume of the solid DE is always the same however deeply the solid is situated. If the weight E is the excess of the weight DE over the gravity of the water F, the effort, force and impetus by which the solid DE descends in the water is measured by the force of the weight E.
Proposition LII
The motive force by which a solid with a specific weight smaller than that of the fluid rises is equal to the excess of the lightness of the solid over the lightness of a volume of fluid equal to that of the solid.
On the other hand, let us suppose that the wood LE and also the water F lack gravity but are shaped by the force of lightness. Both exert an impulse and impetus upwards and attempt to rise. It is shown in the same way that in the perpetual balance or wheel, the greater lightness of the wood DE prevails over and overcomes the smaller lightness of the adjacent fluid F. The balance is tipped from A towards R, raised by a force equal to the difference or excess of the lightness of the wood over the lightness of the water.
Proposition LIII
The motive force by which a light body rises in a heavy fluid must be equal to the sum of the lightness of the solid and the gravity of the fluid.
Changing the hypothesis, let us suppose that the wood F is light and is impelled and moved upwards by an intrinsic principle (Table 3.1, Fig. 12). The adjacent fluid D which is quicksilver is supposed to exert a downwards force only, as required by its greater gravity, and not to impel upwards. Then a perpetual balance or wheel is formed in which the extremity B is always pulled upwards by the positive lightness of the wood F and rises towards R. The opposite extremity is lowered from A towards H, as the nature of gravity requires. These two movements and efforts at the opposite extremities of the balance are contrary. Thus, they do neither neutralize nor oppose each other, but they favour and enhance each other. Consequently, the effort and impetus by which the balance rotates, i.e. by which the wood F rises from the bottom of the mercury, is equal, not to the difference, but to the sum of the force of the lightness F and the faculty of the weight of mercury D.
Proposition LIV
If a solid as well as a fluid exerts lightness and gravity, the motive force by which one of them is raised is equal to the sum of the difference of their lightnesses and the difference of their gravities.
Finally, let us suppose that the wood exerts a force upwards, inasmuch as it is light, and at the same time exerts its innate gravity (Table 3.1, Fig. 12). Similarly, the water D in a vessel not only compresses downwards, inasmuch as it is heavy, but it is not completely deprived of a degree of lightness. A perpetual imaginary balance is formed. Its extremity I is impelled downwards by the excess of the gravity of the water D over the gravity of the wood F. On the other hand, the extremity B is raised by the excess of the lightness of the wood over the lightness of the water. These impulses are contrary and are applied to the same imaginary balance. Consequently, one impulse does not oppose the other. Therefore, all the effort and impetus of the balance, i.e. the force and impetus by which the wood rises in water, is measured by both excesses, i.e. by the sum of the difference of the weights of the water and wood and the excess of the lightness of the wood over the lightness of the water.
Supposition V
After these premises, let us suppose with the opponents firstly that, besides heavy bodies, light bodies also exist in nature. Some of them, as Aristotle said, are simply light, others are relatively light. Fire is said to be absolutely light. Earth or quicksilver or another fluid as heavy as is earth itself, is called absolutely heavy. Other single or mixed intermediate bodies are then found which are called heavy and relatively light altogether. For example, water immersed in mercury is said to be light and to be moved upwards by an intrinsic principle. But the same water, when immersed in oil, is said to be heavy, not light, and to be moved downwards by an internal principle. This can have a double meaning: either the two mentioned contrary qualities are always present and active in the same body of water, or one or the other is found alternately in the water so that water set at the bottom of mercury is light and in no way heavy; on the other hand, the same water when immersed in oil has there gravity and no lightness at all so that the lightness which impelled water from the bottom of mercury with such efficacy remains dormant and extinct. Consequently, in the first meaning water should always retain two contrary qualities, namely lightness and gravity in the same way. Mixed bodies are said to participate in extreme qualities, namely warmth and cold, as grey colours are considered as participating in blackness and whiteness. Consequently, it should be said that in fire which is absolutely light four complete degrees of lightness are found. In earth also there are four degrees of gravity. Air will have three degrees of lightness and one single degree of ponderosity. Water would have one single degree of lightness and three of gravity. Finally, another body between air and water, perhaps like spirit of wine, could have two degrees of lightness and two other degrees of gravity.
Supposition VI
Aristotle moreover supposed that the velocity at which a body rises or falls in different fluid environments is proportional the rarity or consistency of these fluids. For example, if air was ten times rarer, more subject to be pulled apart and more penetrable than water, a same ball of marble would fall a distance of one cubit ten times more quickly in air than in water. If this distance was travelled in air in one single pulsation of the artery, it would be travelled in water in ten pulsations of the same artery. According to the opinion of Aristotle, the same must be said for the ascent of light bodies. After these premises, in the
Proposition LV
It must be shown that fire is not light and does not rise by the force of its positive lightness.
Firstly, the extreme simple bodies, namely fire and earth, or quicksilver or molten gold or any other very heavy body, according to what Aristotle said, if possible, are absolutely heavy and light. Fire thus has four degrees of lightness and no gravity. On the contrary, earth or quicksilver have four degrees of gravity and no lightness. Earth, therefore, is absolutely and completely heavy and fire absolutely light. Thus (according to Prop. 53), the total effort and impetus by which fire rises through mercury or earth falls through fire must be measured by the sum of the extreme forces, i.e. by all the force of lightness together with all the force of gravity. Therefore, the total impetus will be of eight degrees. But this is not true. It is against the assertion of the opponent and against Archimedes. Indeed the bodies which rise in a fluid are raised by a force equal to the excess of gravity of a volume of mercury equal to that of the igneous body immersed into it, over the gravity of fire which is nil. Thus, fire rises through mercury with an impetus of four degrees. Therefore, fire is not carried upwards by the force of its lightness and thus it is not light. Q.E.D.
But a Peripatetic will insist again and say that the velocity exerted by the fire rising through mercury or by the earth falling through fire can be considered as being either of eight degrees or of four ad libitum since we have no reliable measure of one degree of impetus and so his opinion cannot be refuted by way of common sense and experience.
Proposition LVI
To find a measure of a certain degree of impetus relative to which it can be distinguished whether the impetus of the fall of earth through fire or of the rising of fire through mercury is of eight or four degrees.
But let us refute this dodging of the problem. Let an experiment be carried out, not in mercury which is simply heavy, but in water or in air. Water has three degrees of gravity and one of lightness. Thus fire will rise through water at a velocity of three degrees, in mercury with an impetus of eight degrees, and earth will fall through fire eight times more quickly than through water. Moreover, air has one single degree of gravity and three degrees of lightness. Consequently, fire will rise through mercury eight times more quickly than through air. By this reasoning we shall have the measure of one degree of impetus, in rising as well as in falling, which can be compared with the impetus of fire rising through mercury and that of earth falling through fire. From this it will be easy to conjecture whether these velocities of the extreme elements are or are not in a ratio of eight to one by comparing with the velocities exerted in intermediate elements. Although the experiment does not ensure perfect accuracy, it demonstrates sufficiently the fallacy of the Peripatetic hypothesis, however. Although the force and energy with which bodies rise or fall cannot be deduced from the velocity of their upwards or downwards passage, as we will show clearly in due place, they can be assumed with the opponent, to refute him.
Let us then consider intermediate elements such as air and water or other mixed bodies provided with the same degrees of lightness and gravity. It must be demonstrated that none of these bodies which rise has a positive lightness.
Proposition LVII
If air in water exerted lightness only, it would not rise in the water, impelled by its positive lightness.
Firstly, let us suppose that the mentioned elements do not retain together at the same time the two opposite faculties of gravity and lightness but possess successively one or the other depending on their location in different fluid environments. Water suspended in air must be considered as heavy only and not light. If water is immersed beneath quicksilver, then water is light, not heavy. It is even supposed that air or wood immersed in water is light and has no gravity. A vessel RGHS full of water D is imagined in which a mass of air or wood F is immersed (Table 3.1, Fig. 12). According to the hypothesis mentioned above, the water D has no lightness but gravity alone since this water is not supposed to be immersed in another fluid body denser and heavier than itself but is adjacent to air. The air or wood F is supposed by the opponent to rise from G towards R, pushed by its natural lightness. The surrounding water D exerts an effort and impetus downwards from A towards H, as required by the nature of its gravity. We shall thus have two impulses contrary to each other, that of the lightness of the air F of three degrees and that of the gravity of the surrounding water D of three degrees. The sum of these motive virtues, six degrees, will give the measure of the effort and impetus with which the wood F rises through water. But this is false, against what the opponent himself admits, against the demonstration of Archimedes and finally contrary to experience. Indeed, the bodies which are carried upwards in water rise with as much force as the gravity of the volume of water equal to the immersed body exceeds the gravity of this body. It is as if one said that the upwards impetus is measured by the difference in gravity of air and water, of two degrees, and not by the sum of six degrees of the lightness of one and the gravity of the other. Therefore, air or wood cannot be impelled upwards by its positive lightness.
Proposition LVIII
The same is demonstrated supposing that air and water exert both their forces of lightness and gravity.
Secondly, let us suppose that air as well as water always retains the two opposite qualities, i.e. that both are always provided with the same degrees of gravity and lightness. The lightness of the air F is of three degrees, greater than the lightness of one degree of the water D. On the contrary, the gravity of one degree of the air F is less than the weight of three degrees of the mass of water D equal to F. We shall of course have four motive forces opposed to each other and acting in the imaginary balance BI so that none of them can be inactive. All act and impel together. Consequently, according to Propositions 50 and 54, the effort or impetus by which the air F is impelled upwards in the water from G towards R proportionally to its lightness must be measured by the excess of two degrees of the lightness of air over the lightness of the surrounding water. On the other hand, the effort of the water against the air is carried out by the excess of gravity of the water D over the gravity of the air F, also of two degrees. Therefore, the water, while attempting at descending, necessarily expresses and impels the air F upwards. The two differences or excesses of forces are opposite: one impels upwards in the imaginary balance, the other downwards. Consequently, all the effort and the total impetus by which the air F rises in the water must be measured by the sum of these two excesses, which is 4°, and not by the difference in lightness which is 2° only. But this is untrue and against experience, against the assertion of the opponent and against what Archimedes demonstrated, namely: the effort and impetus by which a bubble is carried upwards in water is equal to the difference of the weights of air and water. Consequently, it is not true that positive lightness is involved in this operation.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


