(1)
Mathematics in Naples, Naples, Italy
Deceased
As mentioned above, it is obvious that some bodies are moved by an external and separate motor. One usually searches for what this moving cause does essentially or what effect it provokes in nature. We observe that bodies which move, are impelled, sustain a blow from an external motor, not only are agitated by a movement while being connected to the moving body itself and are led by the latter as if it were by a hand, but, even after withdrawal of the external mover, the moved bodies themselves, left without a guide, continue the movement which was begun. They thus seem to have acquired instruction, discipline, and even force and faculty to be able to complete the movement. Since the subsequent movement also results from another cause rather than from nothing, it is commonly inferred that the cause and the motive force by which the subsequent movement can be completed and continued, remain in the projectile after this was left by the impeller. A force and some sort of motive faculty have been assumed. If it had been impressed by the projecting body in the moved body, an occurring motive quality would of course migrate from a subject into another. This is commonly considered to be absurd. People then have imagined a new impelling cause which is nothing else than the fluid environment itself, such as water or air which is the motor replacing the projecting subject. Therefore, after grasping the mobile, this fluid continues the previous movement by transporting it until, with the extinction of the motive faculty of air, the movement of the projectile is brought to an end. Although this concept is refuted with the strongest arguments by others and mainly by Galileo, I usefully showed the error of this opinion with new arguments which I found by thinking.
It is usual to defend the peripatetic claim in two ways. For some people, a stone, for instance, is thrown by the hand which holds it. The hand, before parting from the stone, propels the ambient air as well as the stone. When no longer held by the hand, deprived of its propulsion, the stone which has by itself no motive force would fall perpendicularly to the surface of the earth as a result of its weight. But it is surrounded everywhere by air previously agitated and set in movement. Therefore, the stone is carried by the ambient air as if it is were by a rapid stream, until the agitation of the air weakens and finally ceases together with the movement of the carried stone. Others belonging to the same peripatetic school say that the air following the projectile, by returning at the highest velocity and with force to refill the space left by the projectile, to avoid the creation of vacuum abhorrent to nature, moves the stone forwards by pressing continuously behind most violently. This is similar to children who propel plum-stones by pinching them between their fingers.
The falsity of this concept will be shown. If the fluid environment, such as water or air, carries the projected body like a stream, after it has parted from the projecting subject, one must admit that air or water was also impelled by the same projecting subject. Such fluid environment is also mobile and has been subjected to a movement of which it was deprived previously. Consequently, when the propulsion by the projecting subject ceases, except if we are willing to accept a migration of the motive faculty from one subject to another, i.e. from the projecting subject to the fluid itself, we are forced to determine the cause of the continuation of the subsequent movement of this fluid itself. Therefore, some other fluid body surrounding the air or the water so far projected and impelled must be found by which the flow can continue and carry with it the included projectile. This external fluid itself should also be impelled by another ambient fluid and so on ad infinitum. The stone, therefore, could not be projected in the air without an agitation of the whole world. Obviously this does not occur and is impossible. A projection is carried out in a bottle full of water and closed hermetically. If the stone was moved forwards by the ambient water after being parted from the projecting subject, although it is admitted that all the water is moved and whirls up to the surface of the container, the external surface of the water contiguous to the glass, if it was deprived of motive virtue, would have to be carried and propelled by the surface of the glass itself which is absolutely immobile. This concept thus is erroneous. Moreover, it is obvious that air or water are little disturbed and not at all moved by a projectile. They remain very quiet. This appears most clearly in water partially tainted by some coloured powder. Then the movement of the water itself can be observed by the displacement of the corpuscles floating in it. At some distance from the projected body they appear to be absolutely at rest. You will observe the same phenomenon in air after choosing a convenient place where the movement and agitation of the dust fluttering in air can be seen. This occurs in a closed room in which sun rays entering through a window make visible the dust fluttering in the air. There the atoms are not agitated by the projectile at a short distance from the projection. Even more, if a projectile falls on a pointed and stable spear-head or is retained by a very thin thread, the reflection of the projectile occurs along its line of incidence. At the same time, the corpuscles floating in the air or in the water and which were contiguous to the projectile, and the ones which surrounded the projectile closely pursue their first movement straight on. It is thus conjectured that the fluid also agitated by the same direct movement cannot generate a movement opposite to the reflection of the projectile, i.e. it cannot carry the projectile backwards while the fluid runs and proceeds forwards.
This appears even more clearly from our arguments against the other concept which invokes the horror of vacuum. The reason why these absurd concepts are retained by some obstinate people is that they acquiesce to the words while ignoring, not perceiving or considering carelessly the facts. If they were more perspicuous, no doubt they would reject this concept. Therefore, it is worthwhile explaining clearly all the problems of the said peripatetic concept.
Unquestionably the fluid in which a projectile moves either undergoes neither condensation nor rarefaction by the nature of such water or it seems to be made of quicksilver, or it can be constricted or dilated in an utmost manner like air.
Proposition I
If a projectile is in a fluid which cannot condense or rarefy, the resistance of the fluid in front where it is to give way is equal to the force of the air behind, returning to fill the space.
Let us assume that, in a fluid of the first kind, a body ABC is moved from A to D (Table 3.1, Fig. 1). Obviously two operations occur. One is the expulsion and removal of the fluid EDF from in front, to make way to the arriving body ABC. The other is the filling of the space behind which the mobile leaves again and again. The fluid is supposed to have a consistency such that it can neither rarefy nor condense at all. Therefore, as much fluid is expelled and removed in front as returns during exactly the same time into the place behind which must be filled. Thus, all the expelled and returning fluid DGILH must be thought of as a series or conglomerate of many very hard globules one of which impels another with an equal force in a continuous and successive movement so that the lines of the movement of these globules describe kinds of spirals or rings surrounding the mobile ABC from its front to its back. Consequently, the fluid leaves the anterior aspect EDF at the same velocity at which it returns behind to fill the space left ABC. The moment and the force of the resistance exerted by the fluid which must be expelled from the anterior position EDF is formed by the force of the density of this fluid and the force of the velocity at which it must be moved. Similarly, the moment of the virtue by which the same fluid returns to the space behind to refill it, is also formed by the density of the same fluid and the velocity at which it must be moved. The densities of the same fluid are equal as are their velocities which have the same strength. Therefore, the moment of the resistance of the fluid to be expelled is equal to the moment of the fluid returning behind. Consequently, the difficulty and the resistance to expelling the fluid from the place EDF is exactly equal to the backwards force exerted by the fluid to refill the space left behind.
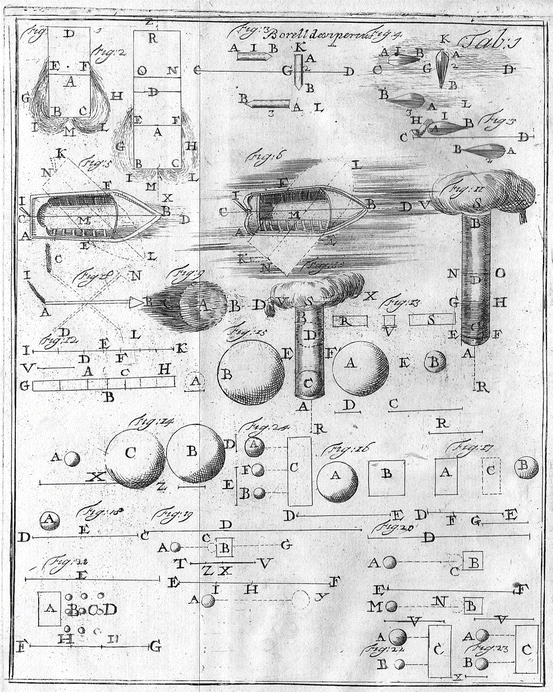
Table 3.1

Proposition II
If we suppose that the fluid body can undergo condensation or rarefaction as is the case in all solid bodies, it is shown that the moment with which the anterior fluid EDF resists expulsion from in front is greater than the moment of the impulse with which the same fluid returns to refill the place left by the mobile body.
Let us assume that the fluid surrounding the projectile is air. Then undoubtedly, during the passage of the mobile ABC from A to C, the air REF in front not only must be expelled from where it is but it must also be condensed for a short time (Table 3.1, Fig. 1). Let us thus suppose that a part DON of the mass of air EONF which must give way to the arriving body ABC is reduced and condensed with another mass of air ORN equal to ABC. Then of course only the residual part of air EDF must run over the sides to refill the space ABC left free. Since the mass of air EDF is smaller than the whole mass EONF, or BAC, it must necessarily rarefy to fill the bigger space ABC, if we do not admit a vacuum. The mass ORN is equal to ABC or EONF and, in it, besides the mass of air present in its normal state of density, another part of air ODN condensed below its normal volume has been introduced. Moreover, the air contained in the space EDF in its normal state, after its rarefaction, refills all the space ABC which is equal to the space ORN. Thus, the ratio of the density of the condensed air ORN in front to the density of the air dilated in the space ABC is equal to the ratio of the sum of the two spaces ORN + ODN to the space EDF. But the force and the energy exerted by the condensed air to dilate are exerted from its centre towards its periphery ORN (in this way it can be restored to its initial dilatation) and inversely the force exerted by the rarefied air to contract is exerted from the circumference towards the centre. It is impossible that the concentrated air in front NRO dilates without propelling and transmitting some force to the mobile ABC by which it was reduced. Conversely, the rarefied air behind, while tending to resume its normal density, cannot propel the mobile ABC when its force and energy, and, therefore, its impulsive movement, are exerted from the circumference towards the centre of its volume. Thus, the air in front opposes and repels by its resistance the mobile ABC moved towards EONF and which strives to remove this air from its place, by as much as it is more concentrated than the air behind. This resistance is greater than the propulsion of the air behind by which the mobile air in front must be moved from M towards D since the ratio of the resistance of the air in front to the impulsive force of the air behind is equal to the ratio of the sum of the two masses RNO + NDO to the mass EDF alone.
So far we compared the resistance of the same fluid with its impulsive virtue, both related to its density. It remains to consider the velocities of these parts of the fluid. Actually, during the same period of time the portion of air EDF is expelled from its position and the space left ABC is refilled. In this space this mass of air is reduced and expanded. The velocities, exerted in the same time, of two fluid bodies having equal masses are in the inverse ratio of the spaces which they occupy and travel through. Thus, the ratio of the velocity of the air EDF in front to the velocity of the air BAC behind is equal to the ratio of the space ABC to the space EDF. The ratio of the moment with which the anterior part of air opposes the progress of the mobile ABC to the moment with which the posterior air returns to refill the space left by the same mobile and with which it propels the mobile, is formed by the ratios of the densities and velocities of the same portions of air, i.e. by the ratio of the sum of the two spaces ORN + ODN to the space EDF, and the ratio of the space ABC or ORN to the same space EDF. Therefore, the ratio of the moment of the resistance of the air in front to the moment of the impetus of the impelling air behind is equal to the ratio of the product of the space ORN and the sum of the spaces ORN + ODN to the square of the space EDF. It is thus obvious that the resistance of the air in front is greater than the impulsive virtue of the air behind returning to fill the space.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


