(1)
Mathematics in Naples, Naples, Italy
Deceased
After having presented the general theorems which are useful to investigate the composition of the movement of heavy bodies and its causes, we arrive at the subject itself. Firstly, we shall consider some principal phenomena of this movement which are obvious.
A heavy body always strives downwards with the same impetus whether starting to fall from a position of immobility or from a movement upwards, downwards or side-ways.
Phenomenon I
If one heavy body is impelled horizontally and another falls simply, both travel the same vertical distances in the same time.
A heavy body B starting from a position of immobility at A and falling freely travels a distance AC in a time T (Table 16.1, Fig. 66). The same body B then is impelled transversely along the horizontal line DE. It arrives at point F in the same time T. During the same time T two motive virtues act, one external which projects the body B horizontally along the straight line DE and the other proper and natural by which the body spontaneously falls vertically. The combination of these movements results in the oblique route DF. EF is drawn perpendicular to ED. The body is impelled by the projecting virtue along the straight line DE and, as a result of the motive force of gravity, it travels the vertical length EF. The body B, if it has a significant specific weight and the distances are short so that the obstacles of air are avoided or are at their smallest, is observed to fall a distance equal to the distance AB which it had travelled at first in a free fall from immobility at A.
Phenomenon II
If a third body is thrown obliquely upwards during the same time with the same impetus, it will travel a horizontal distance equal to the transverse horizontal distance and also a vertical distance equal to the first two.
Then the heavy body B is impelled obliquely upwards, i.e. at an inclination on the horizon (Table 16.1, Fig. 67). Again, in the same time T it travels a distance GH equal to that which was measured horizontally, i.e. DE. This of course corresponds to the equality of the impulsive virtue of the projecting subject. The vertical downwards movement HI travelled in the same time T is also found to be precisely equal to the fall AC starting from immobility.
Phenomenon III
If a fourth body is thrown vertically downwards with the same impetus, it travels in the same time a distance equal to the horizontal and the downwards distances.
Thirdly, the heavy body B is thrown vertically downwards by the same external impulsive force (Table 16.1, Fig. 68). Then of course in the same time T the body travels the straight distance KLM which is precisely equal to the resultant of two distances, one horizontal DE or GH and the other vertical downwards EF or HI. Since the force of the projecting subject is supposed to be always the same, it must necessarily produce the same effect of projection. Thus the fall component KL corresponds to the external impulsive virtue whereas the other component LM is carried out by the innate force of gravity. The descent LM is found to be precisely equal to the distance AC of the free fall begun from immobility.
Phenomenon IV
If finally a fifth body is thrown vertically upwards with the same force, in the same time it will travel a distance equal to the difference between the horizontal and the downwards motion.
Finally the same heavy body B is impelled vertically upwards from a point N by the same projecting virtue (Table 16.1, Fig. 69). It rises up to P. Since the external impulsive virtue is supposed to be always the same, in the same time T it will travel a distance NO equal to KL or GL or DE. The apparent travelled distance NP is observed to be equal to the difference between the impulsive displacement NO and the fall OP equal to AC begun from immobility. Obviously, the downwards movement of the heavy body in the same time T is never altered, i.e. neither increased nor decreased. Therefore, the heavy body B, whatever the movement it carries out whether horizontal or oblique or vertical upwards or downwards, is always of the same magnitude and equal to a free fall begun from immobility.
An easy way by which I demonstrated all that experimentally was as follows. A wheel ABCD was fixed to a wall by a nail about which it rotated in a vertical plane (Table 23.1, Fig. 71). A wooden rod C stuck out of the wheel. Diameters AC and DB perpendicular to each other were drawn and three pipes tangent to the circumference of the wheel were fixed at the extremities D, A, B of the diameters. Their orifices were oriented in the same direction. A nail F was hammered into the wall below so that the wheel could be stopped when the diameter DB was horizontal. After this preparation, the lowest point C of the wheel was brought to the position B and three equal lead balls R, R, R were set in the cavities of the pipes. An assistant sustained a fourth ball R in the position F. Then, after an impetuous rotation of the wheel, its point C was impelled from point B to F. Because of the obstacle of the nail F three projections along straight lines tangent to the circle DAB occurred at the same instant, one vertical upwards DG, one horizontal AH and one vertical downwards BK. Simultaneously, the assistant dropped from point F the ball so far immobile. This ball fell down to M. The projections were chosen short since the collision with air would insensibly slow down and impede their displacements and the fall FM to which the three projections were submitted in the same time. Then a horizontal AI was drawn and a perpendicular IH to it. BL was taken equal to AI and DO was also made equal to AI. The descent BK was found to be equal to the sum F of the horizontal projection AI and the fall IH. The fall FM from immobility was equal to the fall IH or LK, and the vertical rising DG was found to be equal precisely to the difference between AI and IH, as I had foreseen. As a result of the structure of the wheel and of the beginning of the non percussive projecting movement at the same instant, the same degree of impetus was impressed into the three balls R, R, R. If they had had no gravity they should have travelled equal distances DO, AI, BL in the same time. But during this time the force of gravity was acting and pulled these bodies downwards in descents OG, IH, LK. This experiment obviously shows that a heavy body always travels equal downwards distances in equal times (not counting the obstacle of air), whether it starts from immobility or whether it is moving upwards or downwards or side-ways. Moreover, it appears that two movements, one of projection and the other natural, continue and are carried out unaltered by the same body travelling always equal distances in the same time whether the movements are opposite or in any way combined. They never annihilate or weaken each other.
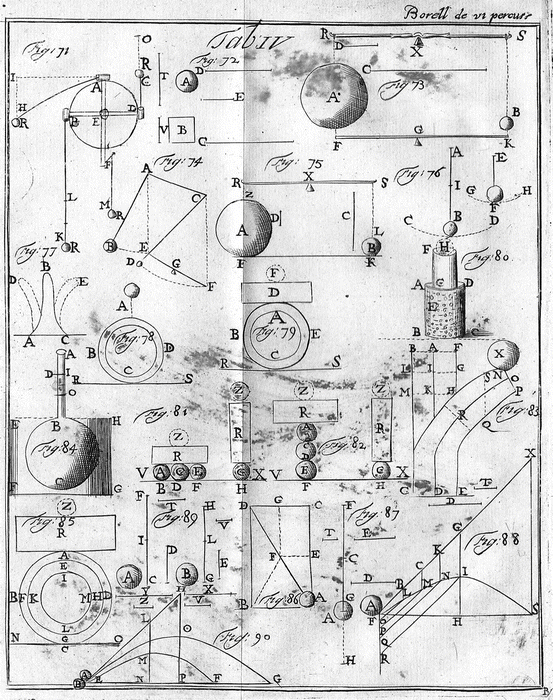
Table 23.1

Proposition LXXXIII
These facts being established, I claim that the purpose of nature in the movement of heavy weights is not a movement, i.e. the force and faculty of gravity do not carry out a movement as such and the motion carried out by a heavy body is not the proper effect primarily intended. It is rather accidental. In itself the effort of gravity is aimed at the immobility of the heavy body at the centre of the earth or at its equilibrium with other heavy bodies about the centre of the earth.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


