(1)
Mathematics in Naples, Naples, Italy
Deceased
Archimedes discussed very precisely and famously bodies sitting in liquid. Later, by another approach, Galileo and Stevin demonstrated the same point, since the truth can be confirmed in countless ways. Myself I devised and presented new demonstrations of these propositions, proceeding in a very different way, not for the pleasure of changing but because they lead to points which must be explained later. But at first some hypotheses must be put forwards.
Supposition I
I firstly suppose that any body, either dense or fluid, among those which compose the terrestrial globe, is heavy and exerts the force or effort of its gravity even if it is a fluid whether homogeneous or not. This, however, will be confirmed in due place by the most obvious reasons and by experiments.
Supposition II
Secondly, I suppose that the force or effort by which fluids tend to unite with the terrestrial sphere is exerted along vertical lines. This results from the fact that any heavy body, by its natural instinct, strives to arrive to the centre of the earth by the shortest way. Consequently, the direction of this movement or compressive effort occurs along radii of the earth. These are perpendicular to the horizon which surrounds the earth spherically. Consequently, it is obvious that the movement or compressive effort of all the parts of a fluid is carried out along perpendicular lines.
Supposition III
Thirdly, it is impossible for any heavy body to move in a spontaneous and natural movement when it cannot approach the centre of the earth. This is obvious, since all the earthy parts in so far as they are heavy bodies, tend to arrive to the centre of the earth by their normal instinct. Their longing desire cannot be satisfied without a movement. Consequently, when the end ceases to be, the means must stop necessarily, i.e. when a heavy body cannot approach the centre of the earth more than previously, it will not move at all. Consequently, these bodies are immobile. If they moved, they would have to recede from the centre of the earth or to circle sideways. In the former instance this would result in an action contrary to the natural instinct of heavy bodies, which is impossible. In the latter instance a vain and frustrating action would be carried out: the heavy body indeed would acquire nothing more since it could not arrive closer to the centre of the earth by hypothesis. Actually, an action of nature carried out by chance and without any goal is absurd and inconceivable. Consequently, bodies unable to come closer to the centre of the earth cannot possibly move at all. Therefore, they must remain immobile in the position in which they were.
Supposition IV
Moreover, Archimedes supposed as a first principle known by itself that the less compressed parts of a consistent fluid which are continuous in the same horizontal plane must be expelled vertically upwards by the more compressed parts of the fluid. This principle actually, although very true, presents, however, with some obscurity since it is not evident why the parts of the fluid can be compressed more or less. Neither is it clear how a natural downwards action must result in an opposite upwards action of another part of the fluid, i.e. a retrogression from the centre of the earth. Consequently, it is worth showing clearly the truth of the mentioned operation and deducing it from better known and more obvious principles.
Proposition I
When a heavy body is not suspended by its centre of gravity, a part of it rises because the whole heavy body falls.
Let a heavy body AB large or made of two parts be located at the extremities of a horizontal balance AB (Table 2.1, Fig. 1). Their common centre of gravity is D. The balance is supported at point C at a distance from the centre of gravity D. I claim that the opposite part B will rise over the arc BF because the whole heavy body AB approaches the centre of the earth more than previously. The two heavy bodies A and B exert their gravity and effort of compression at their common centre of gravity D. This centre of gravity D is remote from the stable support C. Consequently, the whole will behave like a horizontal pendulum suspended from point C whereas all the weight is applied at the centre D at the end of the rope or line CD. But the nature of a pendulum is such that it tends to move downwards over the arc DE of a quadrant about the fixed centre C down to the lowest point E which is closer to the centre of the earth than in the horizontal position D. All this necessary and natural operation obviously results from the descent of all the body. The pendulum CD cannot possibly be brought to its lowest position CE without the rigid balance becoming perpendicular such as GCF. This cannot be achieved unless the less heavy part B of the balance rises upwards over the arc BF. Consequently, the fall and descent of all the heavy body AB from its high position D down to its lowest position E is the actual and regular cause of the ascent of the body B over the arc BF. Q.E.D.
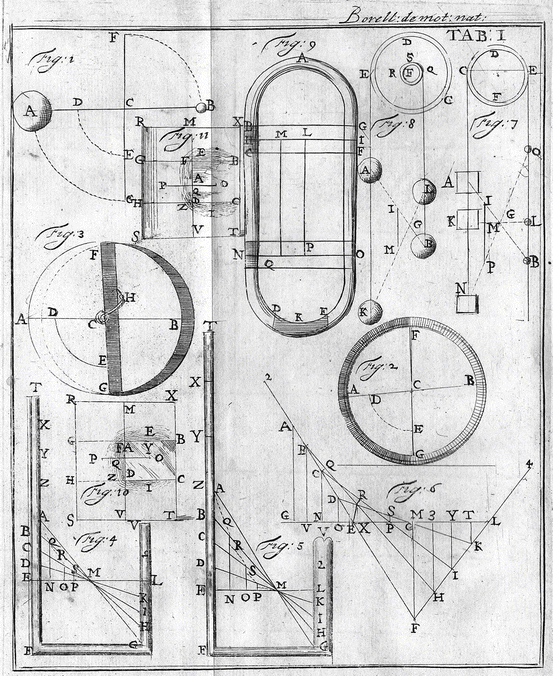
Table 2.1

Consequently, it appears that the simple fall or descent of a heavy body is the actual and regular cause of the upwards displacement and ascent of a part of it. This occurs whenever all the heavy body is supported from an actual or imaginary point of the balance so that the movement of all the parts does not take place along parallel and vertical straight lines but over the circular lines described by a pendulum. In such circular movement, the ascent of the less heavy part B over the arc BF is as necessary and natural as the fall and descent of all the heavy body over the arc DE down to the lowest point E. Although the ascent of the part B is commonly considered as a violent movement, nevertheless if one considers the rotation and the due situation of the heavy body, in so far as this situation is natural and acquired and produced by natural instinct, it is indeed impossible perfectly to attain this due situation without ascent of the part B. Actually, who will the end must also be willing the means which are necessary to attain the end. It is thus logical to infer that the less heavy body is impelled upwards towards F by a natural force. It must, therefore, be admitted that the ascent over BF is natural or rather that the violence of the said upwards movement must be included in a natural operation. Whatever happens, it is sufficient for us that this operation is necessary and cannot occur in another way. Actually, let the others call it either natural or violent, at will.
Proposition II
The same point is verified in fluids contained in a circular siphon.
In order to have two bodies at the extremities of a balance it is not always necessary that the heavy bodies A and B be attached to a rigid and consistent beam such as ACB (Table 2.1, Fig. 2). A circular pipe AGBF can be conceived. When filled with water or another fluid liquid, its right part FAG is heavier than the remaining part of the fluid GBF. If the fluid FAG is quicksilver and FBG simple water, a balance will also be constituted. The centre of gravity of the two liquids will not lie on the vertical diameter FCG but outside it between C and A, i.e. at some point D. The centre of all the quantity of fluid will be C and all the fluid is suspended there. Two opposite movements will occur about C: a descent of the fluid A and an ascent of the opposite fluid B. Since the common centre of gravity D of the two fluids is at a distance from the centre of suspension C, a pendulum results which carries out a circular movement over the arc DE.
Proposition III
Presentation of an instrument in which perpetual motion seems to be carried out, and detection of its shortcoming and insufficiency.
Here, in a short and not completely superfluous digression, I will indicate the impossibility of perpetual motion in a machine which seems to have such likeliness that anybody would swear that movement can be easily continued with such an instrument. My excellent friend Clement, the seventh disciple of Galileo, explained to me in the past this speculation and the structure of this instrument. By looking at winding-drums, or at the wheels by which small boats are pulled at Pisa and in Belgium from one canal to another by the force of one man alone who rotates the wheel by climbing on its inside, as spits are rotated by dogs in a winding-drum in kitchens, he thought that a winding-drum could be made the left half side of which could always be occupied by a liquid heavier than that in the right half. As shown in the diagram (Table 2.1, Fig. 3), the copper winding-drum AFBG is formed by a curved cylindrical surface of copper and two circular parallel flat sheets, perfectly smooth and welded to the cylindrical surface. In the cavity of the drum there is a flat sheet FCG which is used as a partition. Half the cylinder FCGA is filled with water or quicksilver, the other half BFCG with oil or air. The partition FCG is welded to the axis HC inside the drum and can be rotated about the fixed axle C by way of a crank H so as to fit exactly the internal surfaces of the two flat bases and the concave surface of the drum. The rotated partition must be tight like a cap and it must prevent the water or mercury contained in the half cylinder FAG from leaking, whereas the other space GBF remains full of air or oil. The drum is suspended on the axle C resting on two supports so as to be able freely to rotate in a vertical plane. If the hand retained perpetually the crank H and the partition FCG attached to it in a vertical position, we would in this instance unquestionably have a perpetual imaginary balance ACB with equal arms, said my friend, and this balance would be compressed by unequal weights. The arm CA would carry the weight of a half cylinder of mercury or water whereas the opposite arm CB would be compressed by a lighter weight of oil or air. The centre of gravity of these unequal weights would always lie at a point D between C and A. Consequently, the balance AB should always tip to the side A or rather it would constitute a horizontal pendulum CD suspended at the centre C. Therefore, the pendulum should descend over the arc DE. Since the heavier liquid FAG cannot flow downwards, impeded by the partition FCG retained in a vertical position by the hand, all the half cylinder of mercury compressing and climbing the concave surface of the drum AG which is rotatable would impel it. This should rotate downwards from A towards G since it is not impeded by any binding. Consequently, the drum would always be able to rotate from A towards G since the cause of such rotation would always persist, i.e. the pendulum CD would always be maintained in a horizontal position and thus would always compress and climb the surface AG of the winding-drum. Therefore, it seems that such an artifice can result in perpetual movement of the winding-drum.
As I said, this seems so likely that none of the many friends to whom I explained the artifice suspected its deceit. Nevertheless, although I never cared bringing this artifice into practice, I do not hesitate asserting that perpetuity of movement cannot be achieved this way. Indeed I cannot believe that heavy bodies can ever move spontaneously when not even a javelin is able of descending more than previously and cannot approach the centre of the earth. Since the common centre of gravity D of the two fluids is always retained in the same horizontal plane ABCD, it seems impossible to me that the wheel or the winding-drum AGBF rotates in the direction of A towards G. Although the common centre of gravity D is at a distance from the fixed centre of rotation C and thus constitutes a horizontal pendulum, I say that it is retained and suspended by the force of the hand which prevents the partition FG from being rotated by the force of the weight acting at the centre D. It is as if a pendulum CD supported by a subjacent hand could not move downwards over the arc DE. Although, in our instance, the pendulum CD is not something continuous and bound to the centre C, when exerting its effort over the arc DE, it nevertheless behaves exactly as if it had been bound to the centre C. The one who prevents the descent of the heavy body D which can move only over the arc DE necessarily prevents its motive action of displacement. Therefore, it cannot impel the fluid FAG since this is absolutely immobile, nor rotate the drum. One can in no way conceive that a projectile be impelled by a body which is absolutely immobile. Indeed an impeller must be provided with an impetus and movement to be able to impress a degree of impetus into a projectile. Since the quicksilver FAG is absolutely inert and deprived of movement, it appears completely impossible that it succeeds in impressing any degree of impetus into the projected drum. Therefore, the winding-drum is not displaced. Not only a rotatory movement cannot be continued perpetually by this artifice but the artifice cannot even start a movement. After this digression let us return to our matter.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


